Шахматное поле: 64 клетки или 64 квадратика

Кружок 6 класса

Руководитель Евгений Александрович Асташов2012/2013 учебный год

Занятие 20. Раскраски

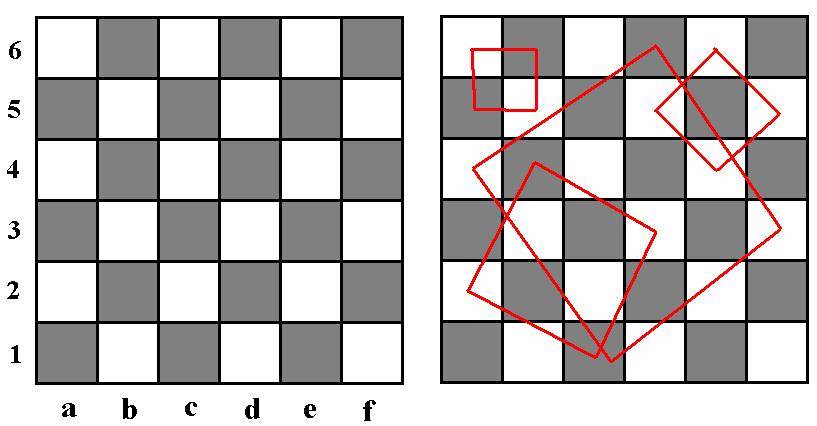
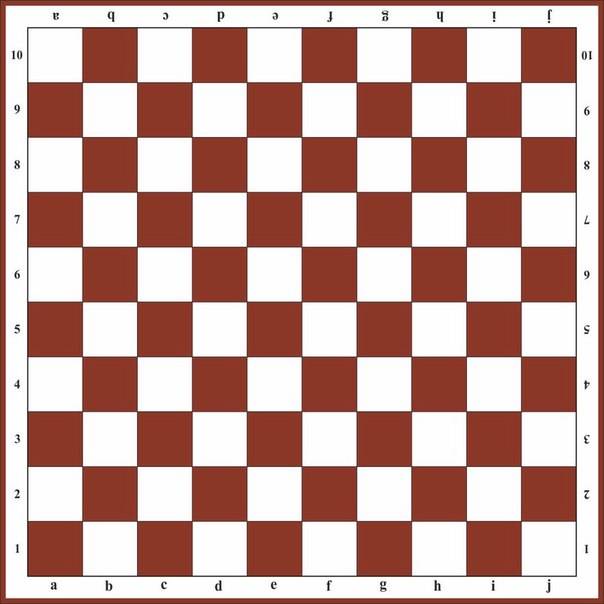
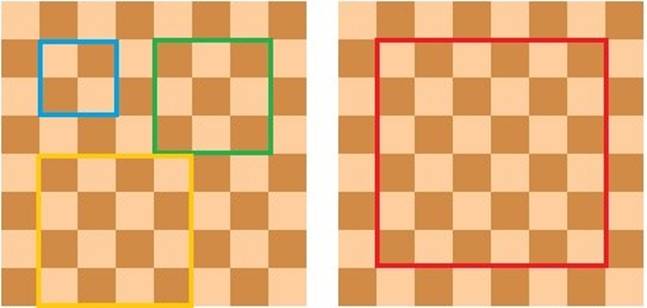
При решении задач этого занятия вам пригодится уже знакомая вам шахматная раскраска, а также следующие двухцветные и многоцветные раскраски:

Раскраска 1	Раскраска 2	Раскраска 3	Раскраска 4	Раскраска 5

Почти все задачи снабжены подсказками.

1.

а)

Из обычной шахматной доски 8×8 вырезали клетки C5 и G2. Можно ли то, что осталось, замостить доминошками 1×2?

б)

Тот же вопрос, если вырезали клетки C6 и G2.

Подсказка.
Используйте шахматную раскраску.

2.

Можно ли разбить квадрат 8×8 с отрезанным уголком на прямоугольники 1×3?

Подсказка.
Воспользуйтесь раскраской 1.

3.

Можно ли доску размером 10×10 клеток разрезать на фигурки в форме буквы T из четырёх клеток, как на рисунке ниже?

Подсказка.
Используйте шахматную раскраску.

4.

Можно ли доску 10×10 разрезать на фигурки из четырёх клеток в форме буквы Г, как на рисунке ниже?

Подсказка.
Воспользуйтесь раскраской 3.

5.

Можно ли квадрат 6×6 разрезать на прямоугольники 1×4? Придумайте раскраску для решения этой задачи самостоятельно.

6.

Доска 8×8 разрезана на доминошки размером 2×1. Может ли быть 15 вертикальных и 17 горизонтальных доминошек?

Подсказка.
Воспользуйтесь раскраской 3.

7.

Можно ли из квадрата 7×7 вырезать 10 квадратов 2×2?

Подсказка.
Воспользуйтесь раскраской 4.

8.

На клетчатой бумаге произвольным образом отмечено 20 клеток. Докажите, что среди них всегда можно выбрать не менее 5 клеток, попарно не соприкасающихся друг с другом. Соприкасающимися считаются клетки, имеющие хотя бы одну общую вершину.

Подсказка.
Воспользуйтесь раскраской 2.

9.

Из листа клетчатой бумаги размером 17×17 клеточек вырезали 35 квадратиков 2×2 (режут по линиям). Докажите, что из оставшейся части листа можно вырезать ещё хотя бы один такой же квадратик.

Подсказка.
Воспользуйтесь раскраской 5.

10.

В левый нижний угол шахматной доски 8×8 поставлено в форме квадрата 3×3 девять фишек. Фишка может прыгать на свободное поле через рядом стоящую фишку, то есть симметрично отражаться относительно её центра (прыгать можно по вертикали, горизонтали и диагонали). Можно ли за некоторое количество таких ходов поставить все фишки вновь в форме квадрата 3×3, но в другом углу:

а)

левом верхнем;

б)

правом верхнем?

Подсказка.
Воспользуйтесь раскраской 3.

11.

Кусок сыра имеет форму кубика 3×3×3, из которого вырезан центральный кубик. Мышь начинает грызть этот кусок сыра. Сначала она съедает некоторый кубик
1×1×1. После того, как мышь съедает очередной кубик 1×1×1, она приступает к съедению одного из соседних (по грани) кубиков с только что съеденным. Сможет
ли мышь съесть весь кусок сыра?

Подсказка.
Используйте шахматную раскраску.

12.

Треугольник разбит на треугольнички (25 штук), как показано на рисунке. Жук может ходить по треугольнику, переходя между соседними (по стороне) треугольничками. Какое максимальное количество треугольничков может пройти жук, если в каждом он побывал не больше одного раза?

Подсказка.
Используйте шахматную раскраску.

Решения

Сумма степеней двойки от нуля до данной положительной целой степени на 1 меньше, чем следующая степень двойки (то есть следующее число Мерсенна ).

Простое решение методом перебора – просто вручную удвоить и добавить каждый шаг в серии:

Т64{\ displaystyle T_ {64}} = 1 + 2 + 4 + ….. + 9,223,372,036,854,775,808 = 18,446,744,073,709,551,615

где – общее количество зерен.Т64{\ displaystyle T_ {64}}

Ряд может быть выражен с помощью показателей:

Т64знак равно2+21+22+⋯+263{\ displaystyle T_ {64} = 2 ^ {0} + 2 ^ {1} + 2 ^ {2} + \ cdots + 2 ^ {63}}

и, представленный с обозначением заглавной буквы как:

∑язнак равно632я.{\ Displaystyle \ сумма _ {я = 0} ^ {63} 2 ^ {я}. \,}

Это также может быть решено намного проще, используя:

Т64знак равно264-1.{\ Displaystyle T_ {64} = 2 ^ {64} -1. \,}

Доказательством чего является:

sзнак равно2+21+22+⋯+263.{\ displaystyle s = 2 ^ {0} + 2 ^ {1} + 2 ^ {2} + \ cdots + 2 ^ {63}.}

Умножьте каждую сторону на 2:

2sзнак равно21+22+23+⋯+263+264.{\ displaystyle 2s = 2 ^ {1} + 2 ^ {2} + 2 ^ {3} + \ cdots + 2 ^ {63} + 2 ^ {64}.}

Вычтите исходную серию с каждой стороны:

2s-sзнак равно264-2{\ displaystyle 2s-s = 2 ^ {64} -2 ^ {0}}

∴sзнак равно264-1.{\ displaystyle \, следовательно, s = 2 ^ {64} -1. \,}

Вышеприведенное решение является частным случаем суммы геометрического ряда, задаваемого формулой

а+ар+ар2+ар3+⋯+арп-1знак равно∑kзнак равноп-1арkзнак равноа1-рп1-р,{\ displaystyle a + ar + ar ^ {2} + ar ^ {3} + \ cdots + ar ^ {n-1} = \ sum _ {k = 0} ^ {n-1} ar ^ {k} = а \, {\ frac {1-r ^ {n}} {1-r}},}

где – первый член ряда, – обыкновенное отношение и – количество членов.
а{\ displaystyle a}р{\ displaystyle r}п{\ displaystyle n}

В этой задаче , и .
азнак равно1{\ displaystyle a = 1}рзнак равно2{\ displaystyle r = 2}пзнак равно64{\ displaystyle n = 64}

Упражнение по работе с этой проблемой может быть использовано для объяснения и демонстрации экспонент и быстрого роста экспоненциальных и геометрических последовательностей. Его также можно использовать для иллюстрации сигма-обозначений . Выраженный в показателях, геометрический ряд будет следующим: 2  + 2 1  + 2 2
 + 2 3  + … и так далее, вплоть до 2 63 . Основание каждого возведения в степень, «2», выражает удвоение в каждом квадрате, а показатели степени представляют положение каждого квадрата (0 для первого квадрата, 1 для второго и т. Д.).

Число зерен – 64-е число Мерсенна .

Вторая половина шахматной доски

Иллюстрация второй половины принципа шахматной доски Рэя Курцвейла . Буквы являются сокращениями для метрических префиксов СИ .

В технологической стратегии «вторая половина шахматной доски» – это фраза, придуманная Рэем Курцвейлом для обозначения момента, когда экспоненциально растущий фактор начинает оказывать значительное экономическое влияние на общую бизнес-стратегию организации. Хотя количество зерен в первой половине шахматной доски велико, количество зерен во второй половине значительно (2 32 > 4 миллиарда раз) больше.

Количество зерен пшеницы на первой половине шахматной доски составляет 1 + 2 + 4 + 8 + … + 2 147 483 648 , всего 4 294 967 295 (2 32  – 1) зерен, или около 279 тонн пшеницы (при условии 65 мг как масса одного зерна пшеницы).

Количество зерен пшеницы на второй половине шахматной доски 2 32 + 2 33 + 2 34 + … + 2 63 , итого 2 64  – 2 32 зерна. Это равняется квадрату количества зерен на первой половине доски плюс само количество зерен. Только первый квадрат второй половины содержит на одно зерно больше, чем вся первая половина. Только на 64-м поле шахматной доски будет 2 63 = 9 223 372 036 854 775 808 зерен, что более чем в два миллиарда раз больше, чем на первой половине шахматной доски.

На всей шахматной доске будет 2 64  – 1 = 18 446 744 073 709 551 615 зерен пшеницы, весом около 1,199 000 000 000 метрических тонн . Это примерно в 1645 раз больше, чем мировое производство пшеницы (729000000 метрических тонн в 2014 году и 780,8 миллиона тонн в 2019 году).

Расположение фигур на доске

Фигуры в шахматах, так же как и поля, имеют два основных цвета: «белый» и «черный». У каждого игрока в начале игры должны быть одинаковые наборы боевых единиц, в которые входят:

• король (царь, князь);
• ферзь (королева, министр, ученый);
• две ладьи (башни, туры);
• два коня (всадника, рыцаря);
• два слона (офицера, епископа);
• восемь пешек (пехотинцев).

В разных культурах термины могут отличаться друг от друга, общепринятые международные названия приведены здесь без скобок. Нажимайте на них, чтобы узнать то, как ходят эти фигуры.

Далее обратите внимание, как расставляются шахматные фигуры:

Доска размещается таким образом, чтобы поле a1 находилось относительно одного из игроков в левом нижнем углу. Фигурами заполняются крайние горизонтальные ряды:

• белые расставляют на 1 и 2 рядах;
• черные на 7 и 8 рядах.

В «защищенном» центре белых размещают короля (e1) и ферзя (d1), рядом с ними слонов, за ними коней, по краям (a1,р1) ладьи, второй ряд состоит из пешек. Фигуры черных должны быть расположены симметрично в рядах 7 и 8.

Никогда нельзя путать расположение горизонтальных рядов и вертикальных, проверять это легче всего по полю a1. Так же как и клетки, фигуры должны быть на своих позициях: ферзь всегда находится на поле своего цвета (белый на белом поле (d1), черный на черном (d8)), а король справа от него.

Удобнее начинать расстановку с центральных полей и главных фигур: короля и ферзя. Ценные участники битвы заслуживают большего внимания, не правда ли? Можно включать дополнительные инструменты восприятия, голосом проговаривая позиции, на которые вы расставляете фигуры.

Запоминание ценности короля, ферзя и других фигур поможет с большим пониманием отрабатывать специальные упражнения, в которых потребуется расстановка на определенные (не стартовые) позиции.

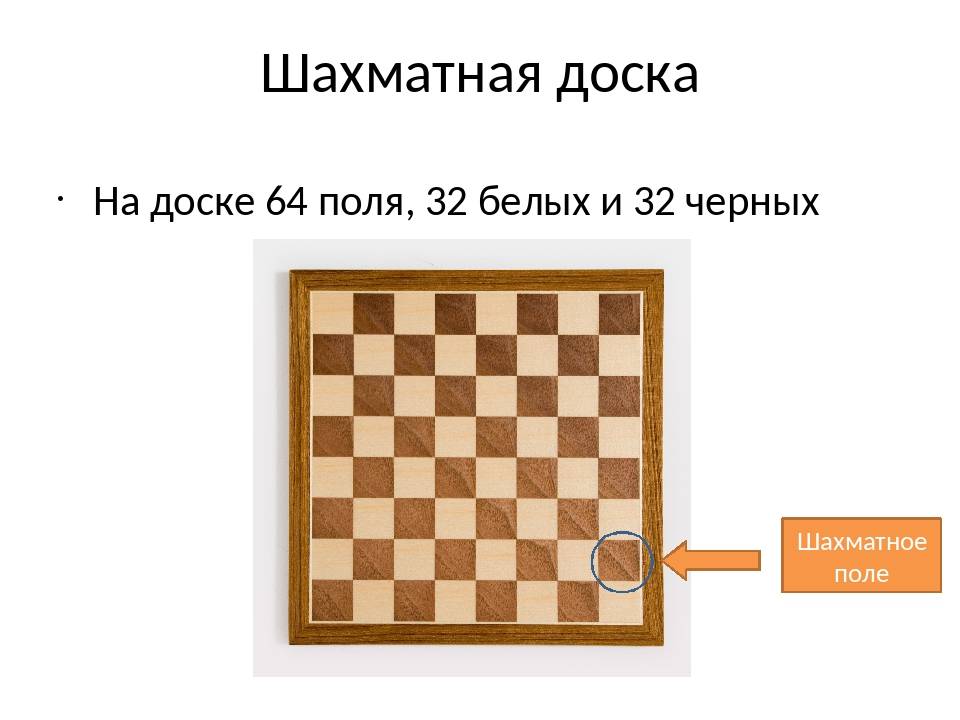
Презентация на тему: ” На каждой шахматной доске 64 поля двух цветов. На самом деле цвета могут быть любого оттенка, но игроки должны хорошо понимать, какие из полей белые,” — Транскрипт:

2

На каждой шахматной доске 64 поля двух цветов. На самом деле цвета могут быть любого оттенка, но игроки должны хорошо понимать, какие из полей белые, а какие чёрные, и правильно расставлять фигуры. Клетки могут быть любых цветов, например одни белые, а другие чёрные, главное, чтобы их было легко различить. Светлые поля всегда называют белыми, а темные чёрными, чтобы не возникало путаницы.

3

Всего на шахматной доске 64 клетки 32 белые клетки и 32 чёрные, поровну. Когда двое противников садятся играть в шахматы, они кладут доску между собой так, чтобы угловая клетка слева от каждого игрока была чёрной. Положи перед собой шахматную доску. Правильно ли ты это сделал? Чтобы проверить, посмотри, какого цвета клетка в левом углу. Она должна быть чёрной.

4

Задача о кляксах На некоторых клетках поставлены цветные кляксы. Они помогут проверить, насколько хорошо ты разбираешься в географии Шахматной страны. Разумеется, на настоящей доске нет никаких клякс ни цветных, ни даже чёрно- белых. На какой клетке стоит красная клякса? А жёлтая? Зелёная? Синяя?

5

Давай поближе познакомимся с шахматной доской. Восемь рядов идут слева направо. Эти ряды обозначены цифрами. Столбики клеток на шахматной доске идут снизу вверх, они обозначаются латинскими буквами. Зеленым квадратиком на доске обозначен центр поля.

6

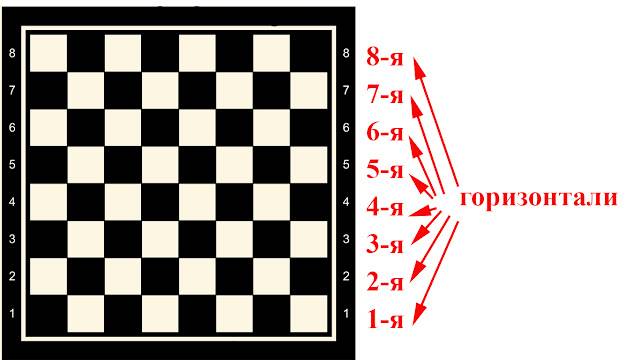
, И АЛЬ Ты видел, как солнце заходит за край леса или моря. Говорят, что солнце заходит за горизонт. Восемь рядов идут слева направо. Эти ряды обозначены цифрами и называются горизонталями.

7

Положи палец на любую клетку возле левого края доски. А теперь проведи пальцем по всем клеткам слева направо он «прошёл» по дорожке из восьми клеток. Это горизонтальная линия.

9

Столбики клеток на шахматной доске, идущие снизу вверх, называются вертикалями. Например, все деревья растут снизу вверх. Вертикали обозначаются латинскими буквами.

10

Такие же дорожки ведут от тебя в сторону противника. Они называются вертикальными линиями. Вертикалей, как и горизонталей, восемь. Проведи пальцем по каждой вертикали.

12

Косые линии доски, проходящие через поля одного цвета, называются диагоналями. Шахматные диагонали бывают белые и чёрные. Диагонали разные по длине. Бывают совсем маленькие. Диагональ, проведённая из угла в угол, называется большой диагональю.

13

Конечно, горизонтали и вертикали – самые главные линии шахматного королевства. Но нужно знать не только о них. Есть и другие линии. Видишь, как клетки одного цвета соприкасаются углами? Прямые цепочки таких клеток образуют диагонали. Диагонали не похожи на другие линии. В каждой диагонали все клетки одного цвета. Ещё одно отличие заключается в том, что все горизонтали и вертикали имеют одинаковую длину, а диагонали разную. Проведи пальцем по всем диагоналям и сосчитай их. Какие диагонали самые длинные? А какие самые короткие? В большой белой диагонали и большой чёрной диагонали по восемь полей. Там, где они пересекаются, находится центр шахматной доски. Это квадратик из четырёх клеток двух белых и двух чёрных.

15

Чтобы знать местоположение шахматных фигур. Зачем нам надо знать правильное название шахматных рядов, столбиков и диагоналей?

Кружок 6 класса

Руководитель Елена Анатольевна Чернышева2005/2006 учебный год

Шахматы и доски. Занятие 17. (18.03.2006)

1.

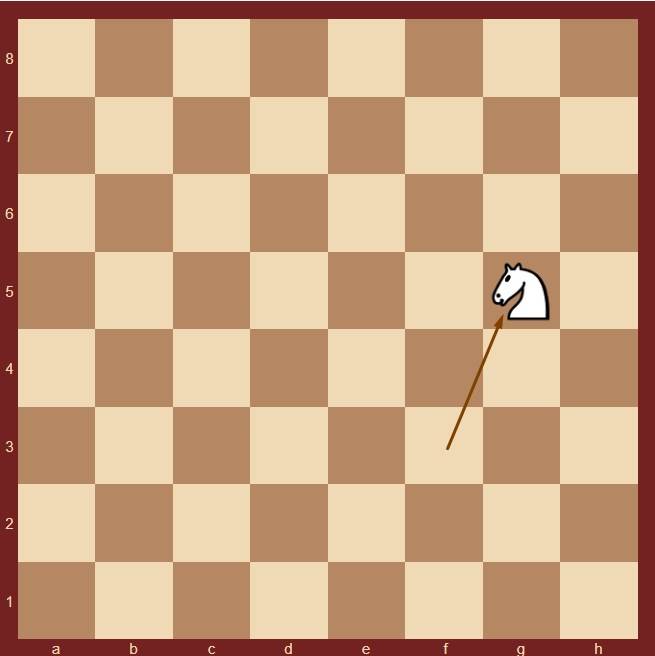
Шахматный конь стоит в левом нижнем углу доски. Может ли он через а) 4; б) 5; в) 1803 хода вернуться на исходное поле?

Ответ Решение

Ответ.
а) да; б) нет; в) нет.

Решение.
в) Нет, так как при каждом ходе конь меняет цвет поля, значит, после нечётного числа ходов он может оказаться только на поле противоположного цвета.

2.

Из шахматной доски вырезали две противоположные угловые клетки. Можно ли разрезать оставшуюся часть на доминошки?

3.

В каждой клетке треугольной доски размером 7 × 7 × 7 сидит жук. В один прекрасный момент каждый жук переполз на соседнюю по стороне клетку.
а) Докажите, что хотя бы одна клетка оказалась при этом свободной.
б) Какое наименьшее число клеток могло оказаться свободными?
в) Задача-конкурс. Придумайте такое «переползание» жуков, чтобы как можно больше клеток оказались пустыми.

Ответ Решение

Ответ.
б) 7.

Решение.
Раскрасим клетки доски в шахматном порядке. Тогда жуки, которые сидели на чёрных клетках, после переползания окажутся на белых, и наоборот. Поскольку клеток одного цвета на 7 больше, чем другого, останется по крайней мере 7 пустых клеток.

4.

Можно ли разрезать шахматную доску на доминошки так, чтобы никакие две доминошки не образовали квадрат 2 × 2?

Указание.
Противоречие легко получить, если попробовать разрезать доску, начиная с угла.

5.

Какое наибольшее число а) ладей; б) королей можно расставить на шахматной доске, чтобы они не били друг друга?

Ответ Решение

Ответ.
а) 8, б) 16.

Решение.
а) Так как в каждом столбце может стоять не больше одной ладьи, то ладей не может быть больше восьми. Восемь ладей можно поставить, например, на одну из диагоналей.
б) Разобьём доску на 16 квадратиков 2 × 2. Тогда в каждом из них может стоять не больше одного короля. Значит, всего на доске не может быть больше 16 королей. 16 королей можно поставить, например, в левых верхних углах таких квадратиков.

6.

На каждом поле доски 11× 11 стоит шашка. Настя и Лена играют в такую игру. За один ход можно убрать одну шашку или любую «полоску» из шашек (несколько шашек, расположенных подряд без пропусков в столбце или строке). Проигрывает тот, кто не может сделать ход. Может ли одна из девочек ходить так, чтобы всегда выигрывать, как бы ни старалась её победить соперница?

7.

Можно ли разрезать шахматную доску на 15 вертикальных и 17 горизонтальных доминошек?

Ответ Решение

Ответ.
Нет.

Решение.
Допустим, так разрезать можно. Раскрасим доску на чёрные и белые горизонтальные полосы. Тогда вертикальные доминошки займут 15 чёрных и 15 белых клеток. Соответственно, горизонтальным доминошкам достанется 49 чёрных и 49 белых клеток. Но каждая горизонтальная доминошка занимает две клетки одного цвета, значит, все горизонтальные доминошки должны занимать чётное число чёрных и чётное число белых клеток. Получили противоречие.

Что такое шахматная доска

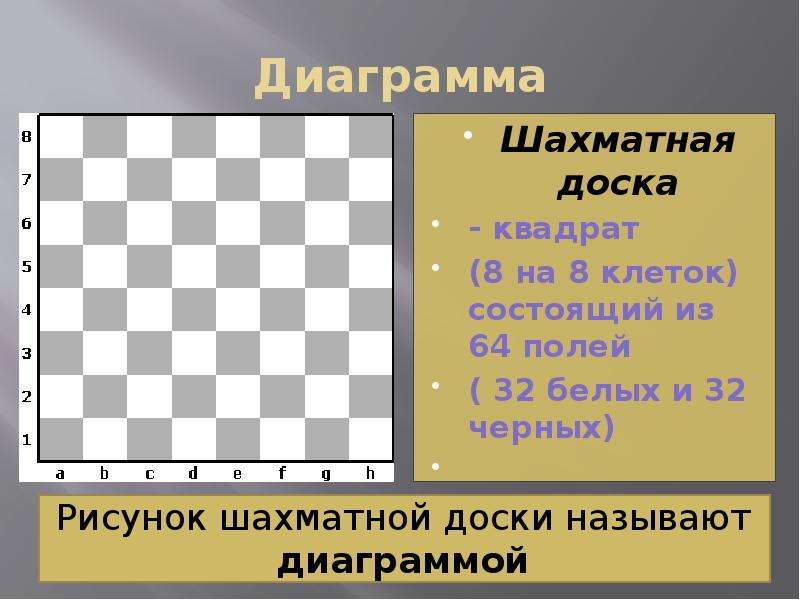
Игровое поле или шахматная доска представляет собой плоскость, разбитую на одинаковые квадратные клетки (поля). В традиционной игре размер доски ограничен: она состоит из 64 клеток, расположенных одинаковыми рядами по 8 клеток в каждом. А вот математики в своих задачах могут использовать шахматную доску любого размера, даже бесконечную.

Сколько клеток на шахматной доске?

Поскольку мы говорим о классических шахматах, на нашей шахматной доске всегда будет ровно 64 клетки

Важно знать, что в зависимости от контекста шахматным полем может называться как вся игровая плоскость, так и отдельная ячейка

Черные и белые поля на шахматной доске

Игровые поля окрашены в два типа цветов: темные и светлые. Это могут быть сочетание темно-коричневых и светло-золотистых клеток, черных и белых, шоколадных и светло-бежевых. В электронных вариациях цвета могут быть любыми, обязательно лишь сохранение контраста светлого и темного. Светлые и темные поля чередуются через одно. Такое расположение в честь самой игры получило название «В шахматном порядке».

Вертикали, горизонтали и диагонали

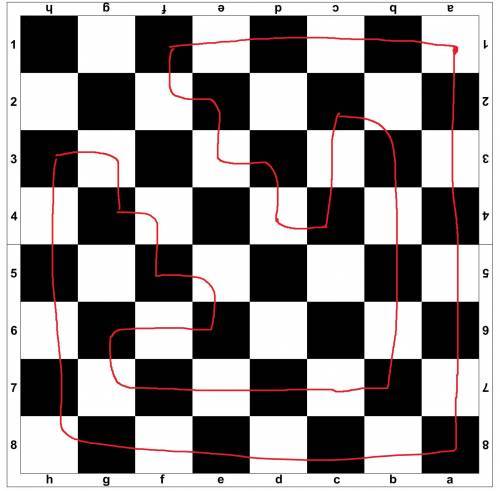
Клетка на доске — основная единица игрового поля. Совокупность из восьми клеток — ряд, который в зависимости от расположения на доске называют вертикальным («вертикаль») или горизонтальным («горизонталь»). Горизонтальным рядам присваиваются номера от 1 до 8, а вертикальные принято обозначать буквами латинского алфавита от A (a) до H (h). Таким образом появляется возможность дать каждой клетке уникальный адрес (номер), состоящий из цифры и буквы. Позиция клетки определяется сочетанием номера горизонтального и вертикального ряда, на пересечении которых располагается ячейка: a1, d6, e8 и так далее. Если рассматривать шахматное поле в целом, можно найти общее с обычной системой координат, в которой по осям располагаются шахматные клетки (поля).

Координаты шахматной доски

Количество клеток, цвет и обозначение полей, безусловно, неслучайны. Порядок игры и каждый ход игрока в партиях, комбинациях, этюдах можно записать, используя условные обозначения. Такую систему называют шахматной нотацией. Удобно, что с помощью сложного обозначения можно легко определить кто из игроков сделал какой ход.

Вначале «шифра», записывается порядковый номер хода, затем указывается белые («.» — точкой) или черные («…»- многоточие) выполнили ход. А далее само содержание смены позиции: буква, обозначающая фигуру, координаты клетки с которой сделано перемещение, и через тире координаты новой позиции на игровом поле.