Положение доски

Цели и функции занесения на доску почета

Виды поощрений трудящихся перечислены в статье 191 ТК РФ. И занесение фото сотрудника на доску почета не упомянуто. Несмотря на это рассматриваемый инструмент поощрения часто применяется в крупных организациях и госучреждениях. Процедура предполагает занесение фотографии сотрудника, его ФИО и специальности на специальный стенд.

Почетная доска наделена этими функциями:

• Выражение одобрения трудовых достижений сотрудников.
• Стимулирование увеличения трудовых показателей.
• Проявление уважения к работе сотрудников.

Предприятие с подразделениями может учредить общую доску почета, а также отдельную доску для каждого подразделения. На стенде фиксируются фото и ФИО сотрудников, которые внесли наибольший вклад в работу компании, как-либо отличились в рамках трудовой деятельности.

Кроме того, организация может утвердить современную доску почета в электронной форме. Размещается она на сайте фирмы. Порядок занесения на нее сотрудников регулируется внутренними актами. Электронная доска – это наиболее комфортный вариант. Занесение сотрудников на нее – дело нескольких минут.

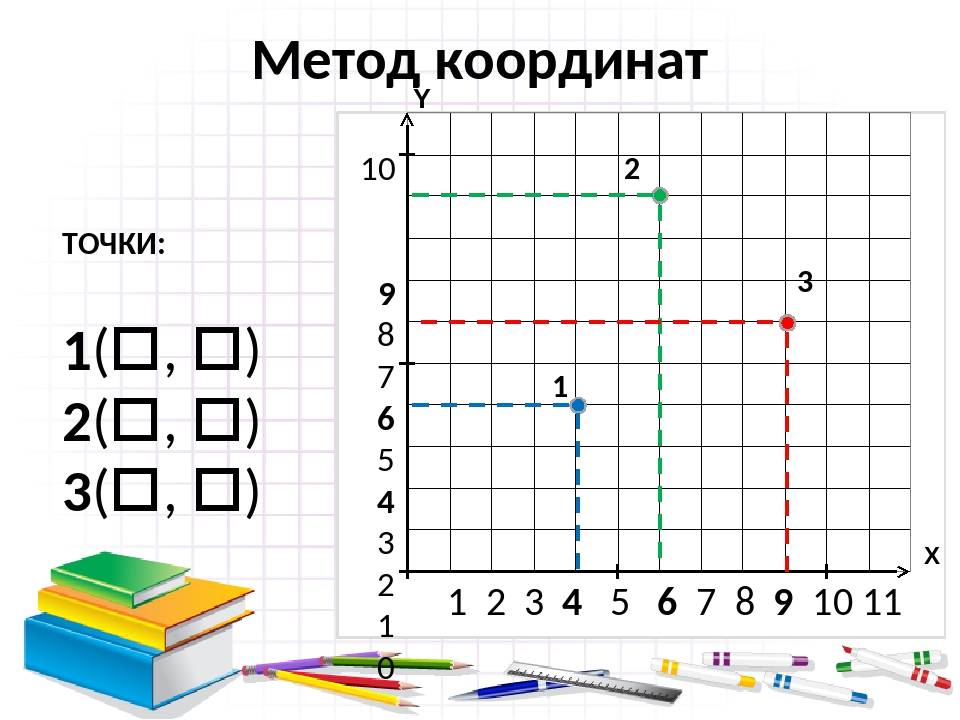
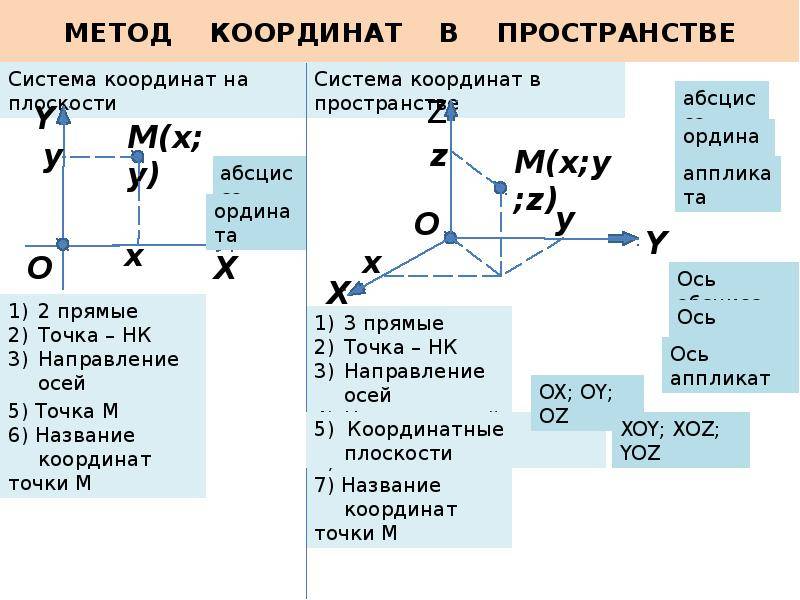
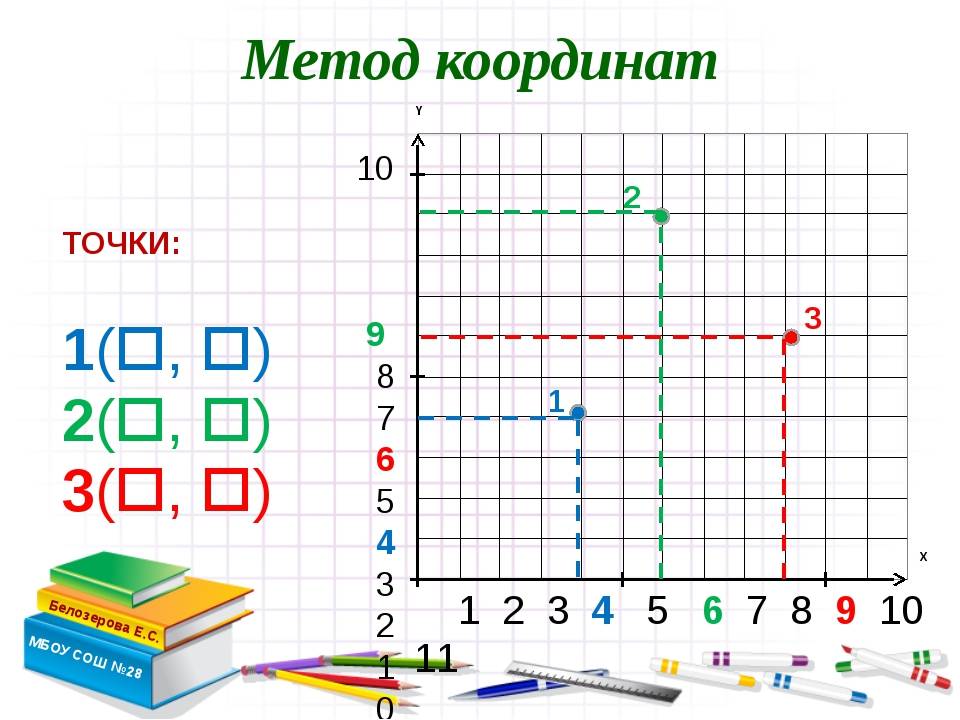
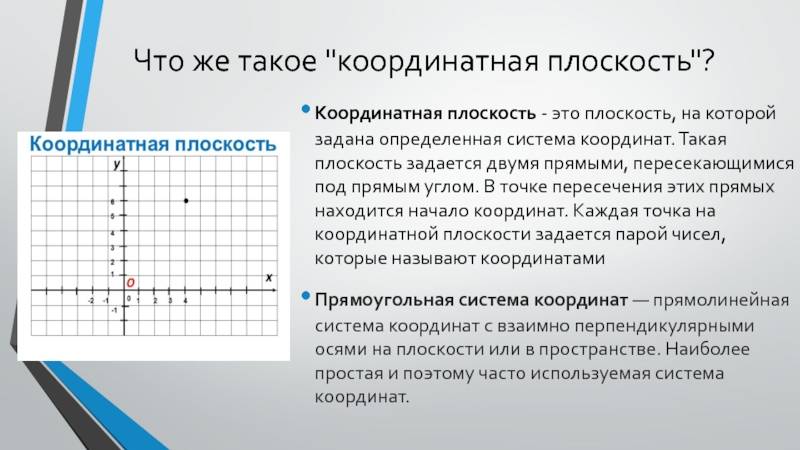
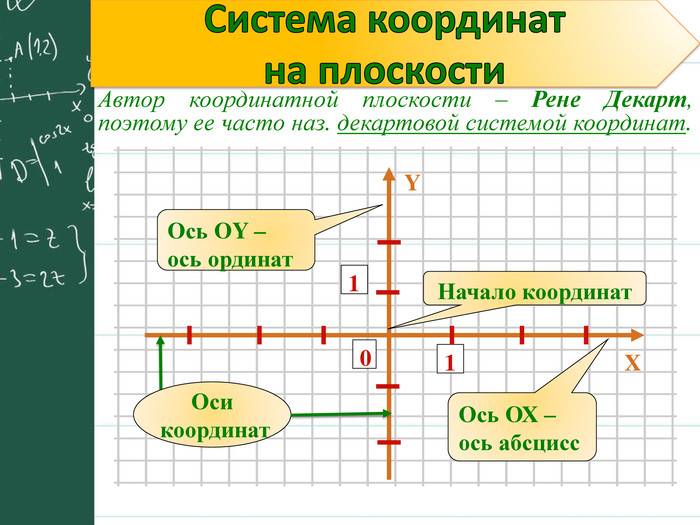
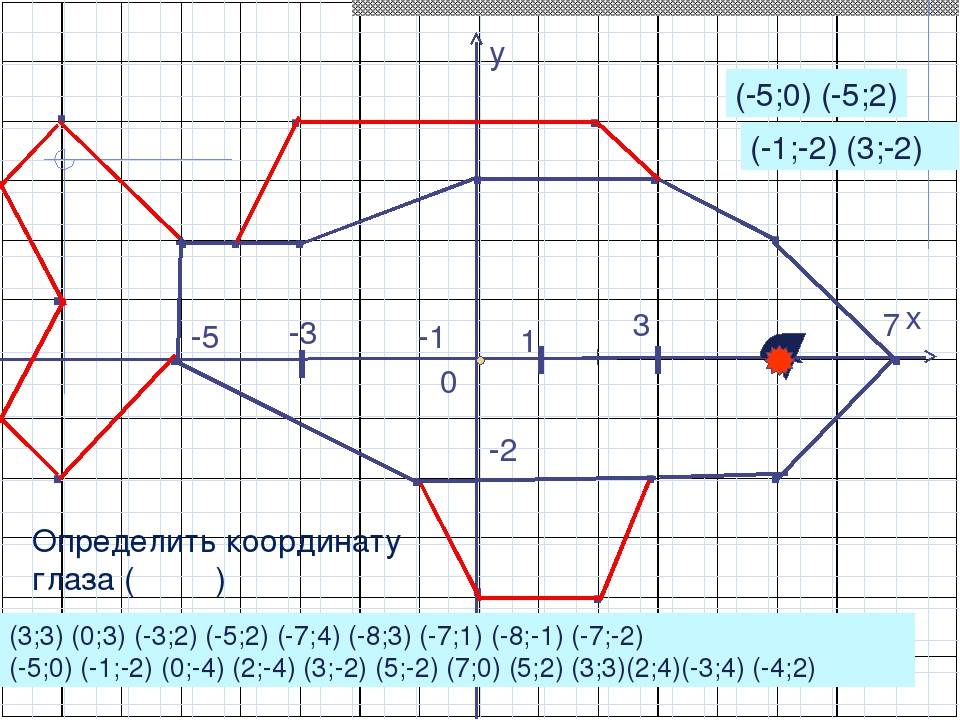
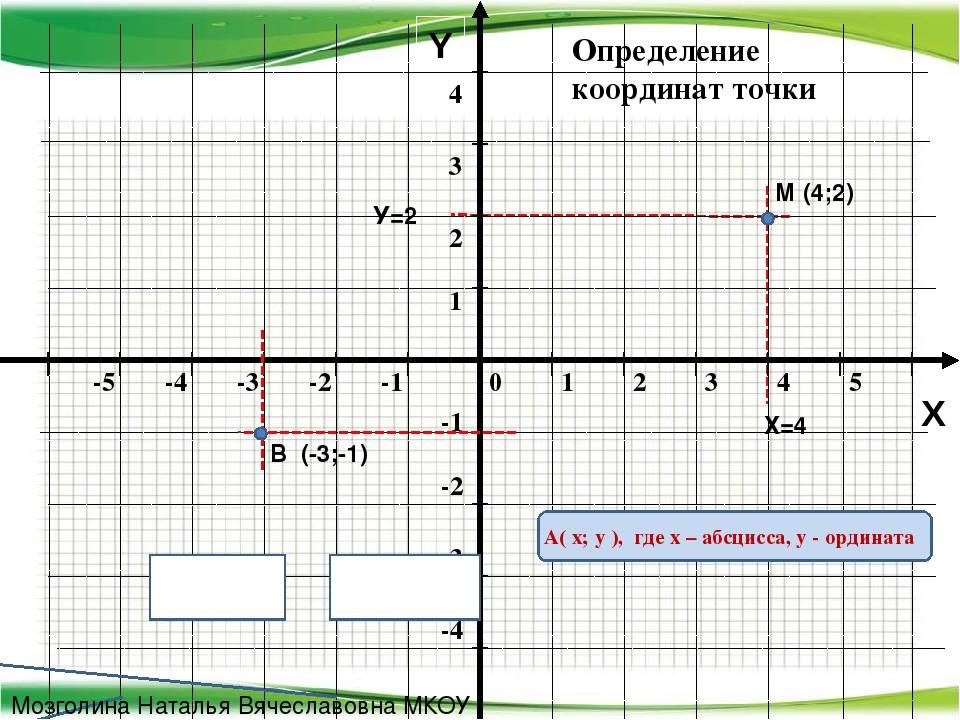
Расположение на плоскости

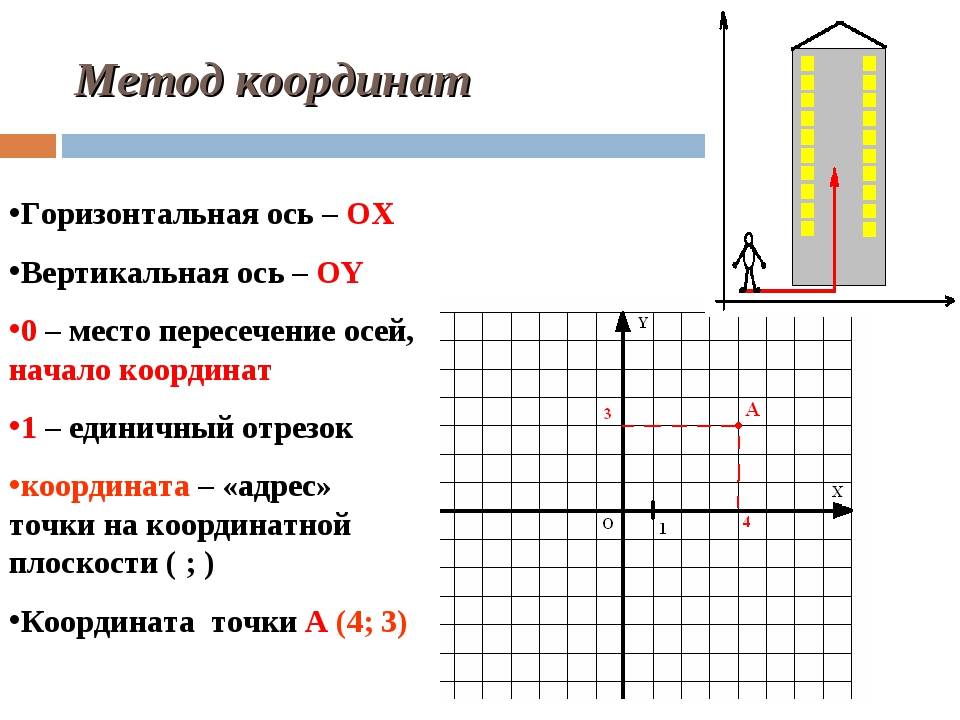
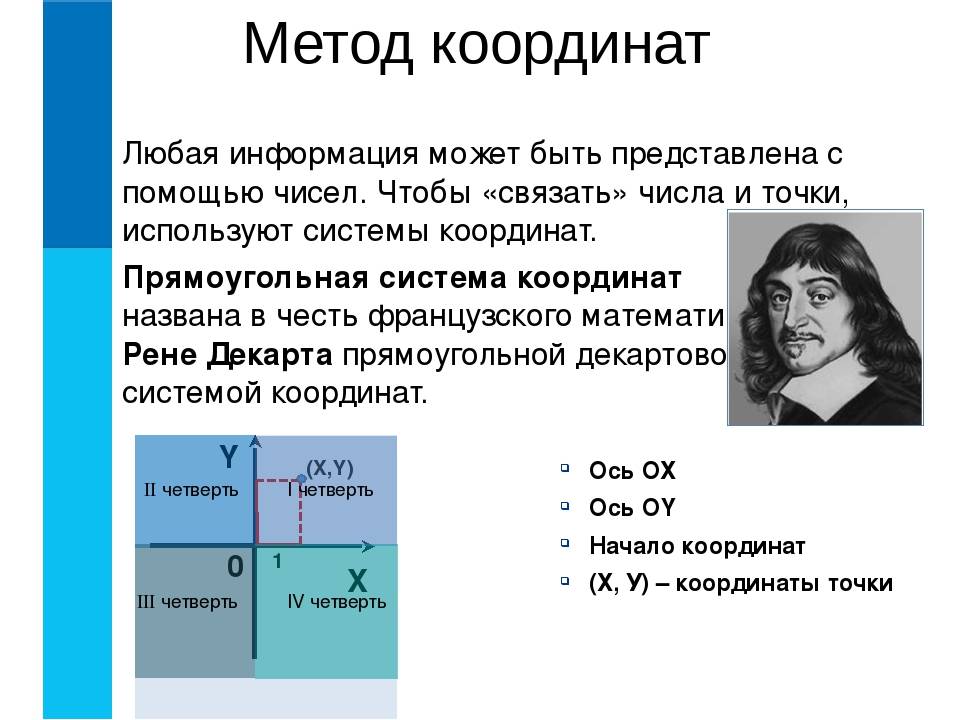
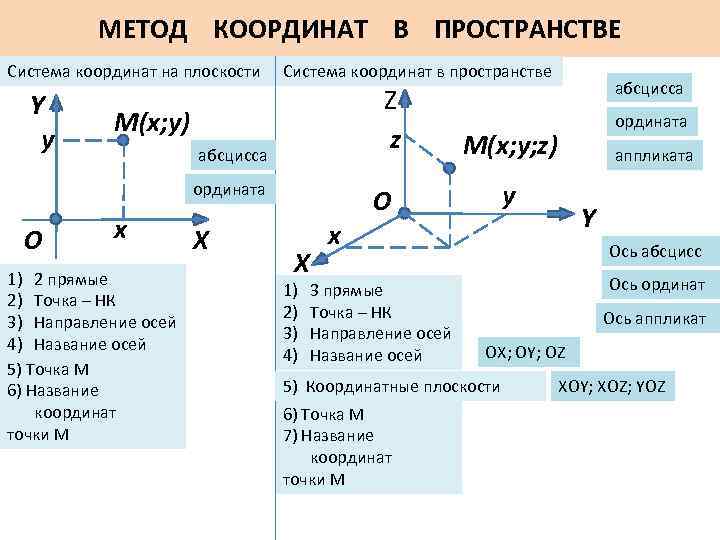
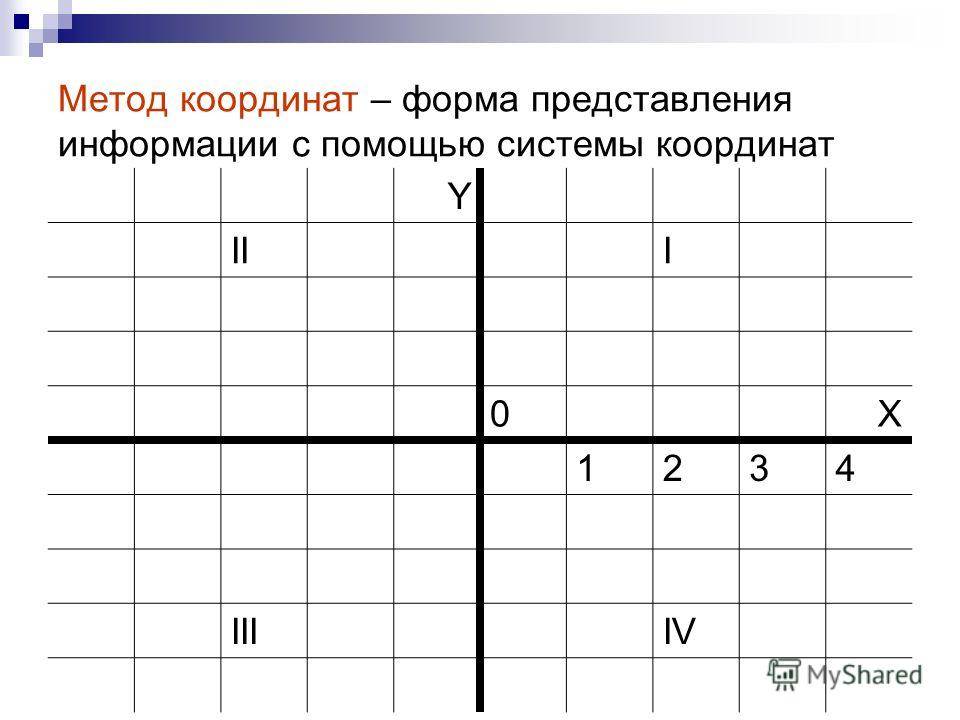
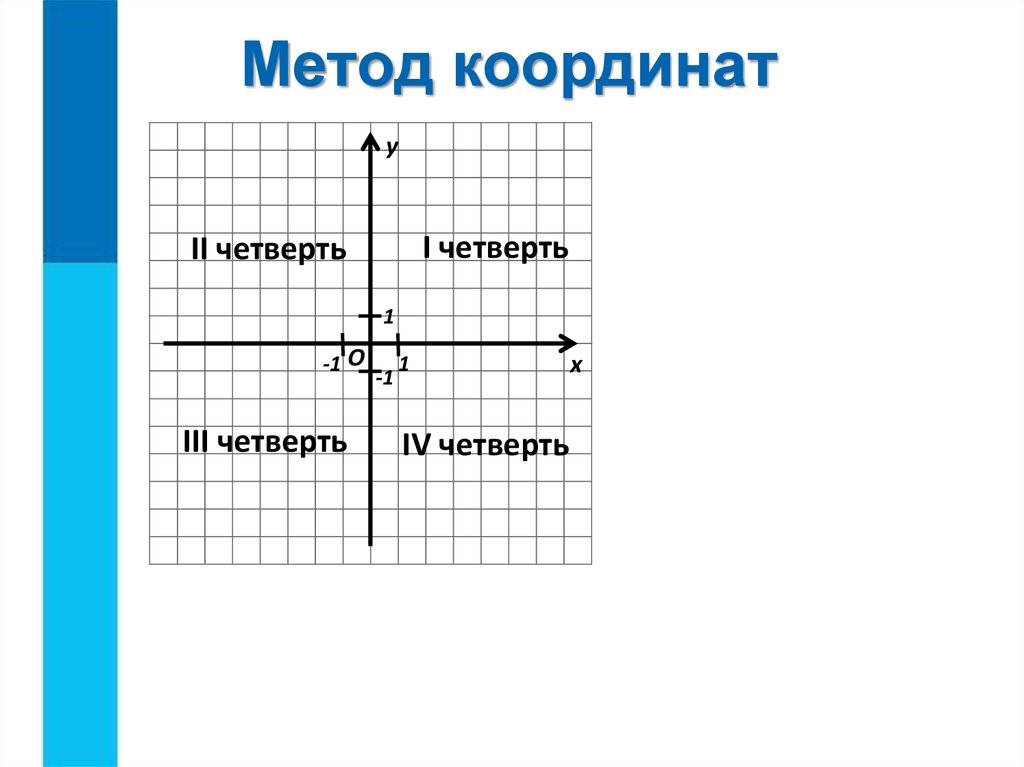
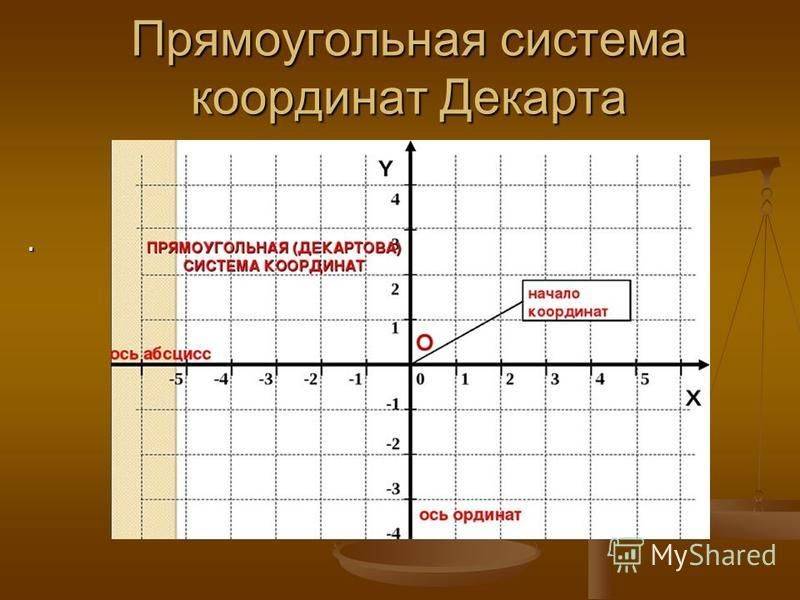
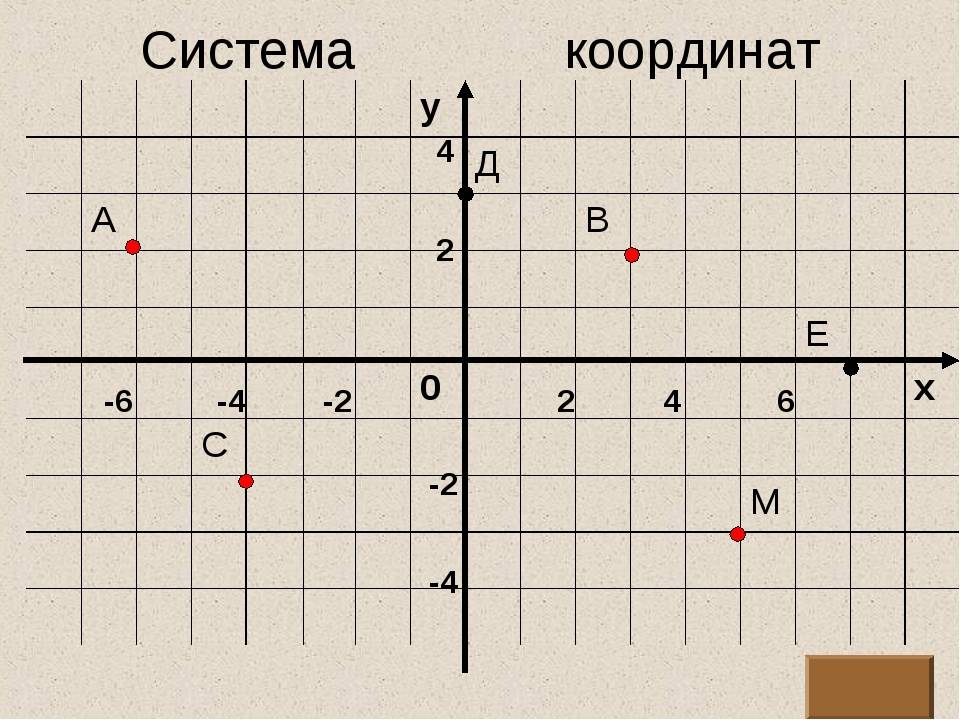
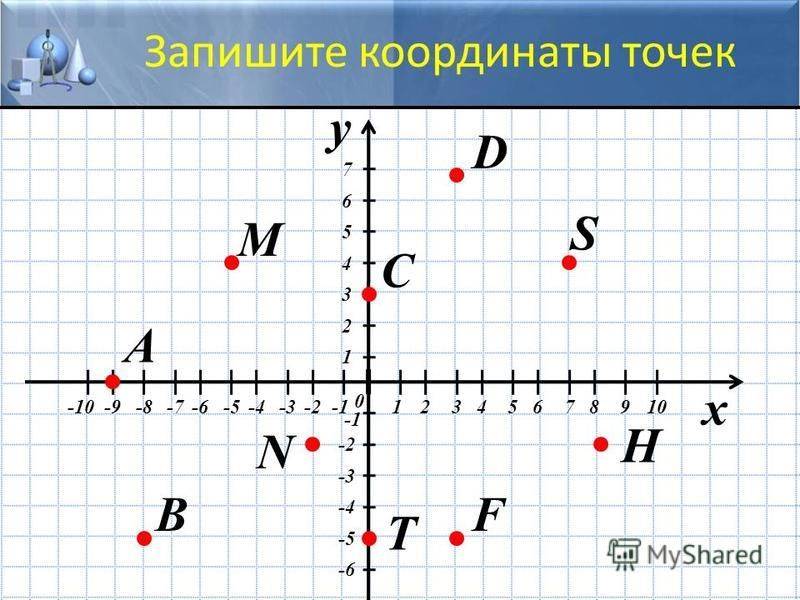
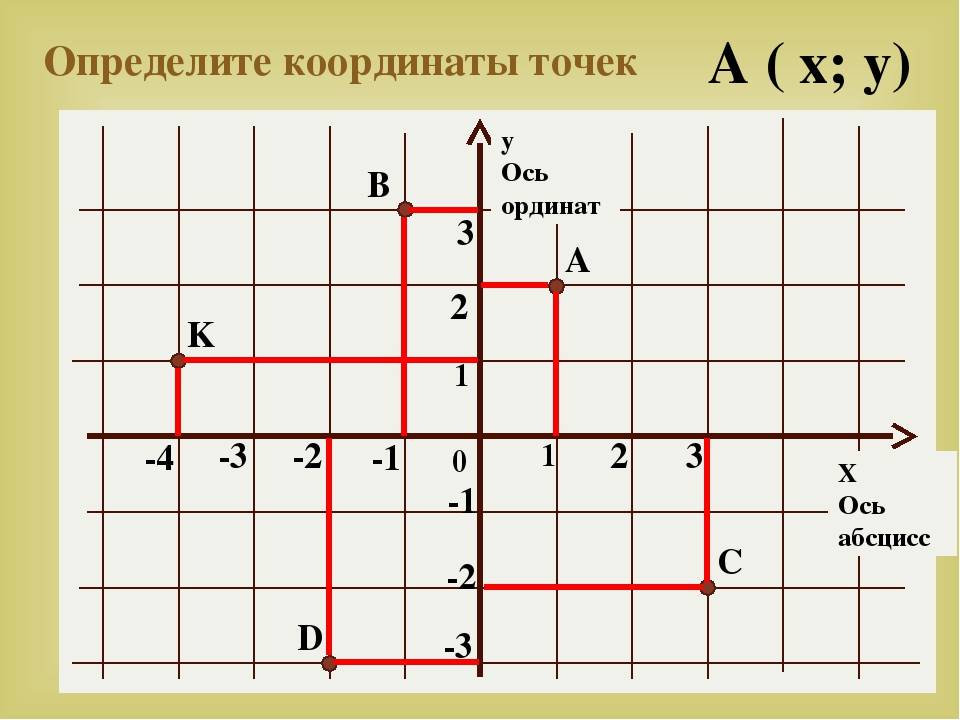
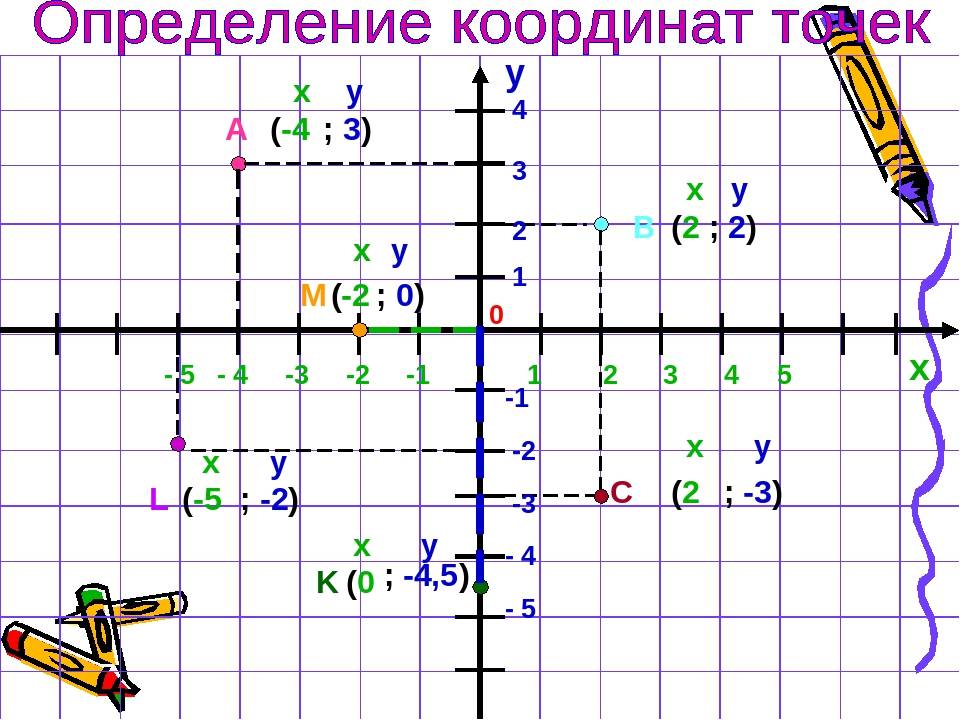
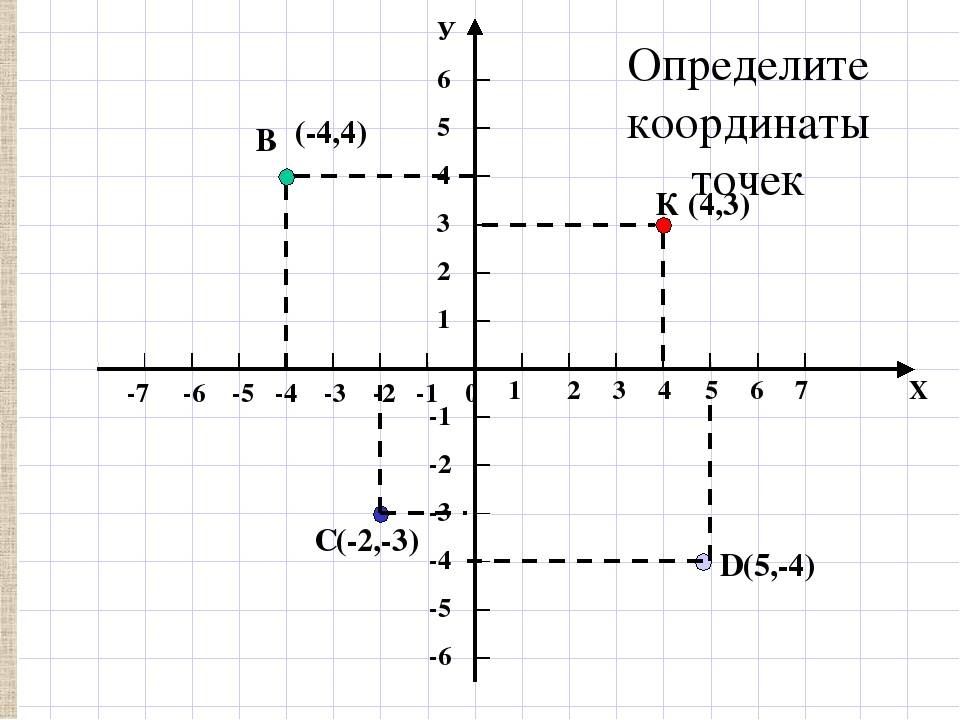
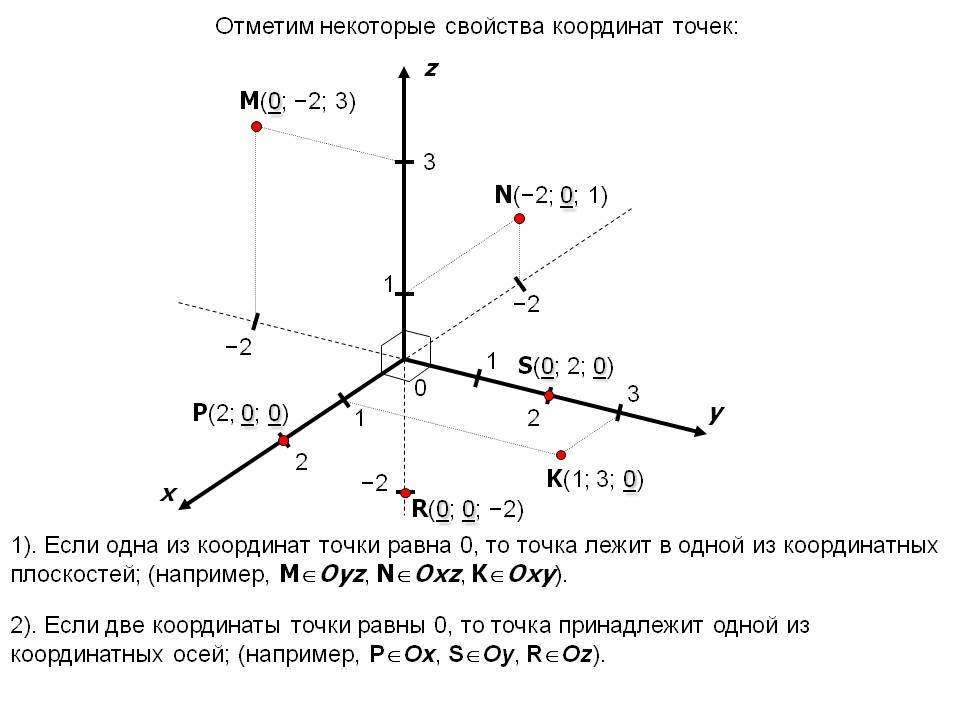
Пусть существуют две плоскости, образующие между собой прямой угол. Их точка пересечения A является началом отсчёта любой из них. Если ось одной плоскости обозначить за X, а второй — за Y, то общим для них пространством будет Axy. Ось, совпадающая с X, называется абсциссой, а Y — ординатой. Единица длины для них одинакова. Пересекающиеся оси образуют четверти. Нумерацию принято вести с верхней правой части против часовой стрелки.

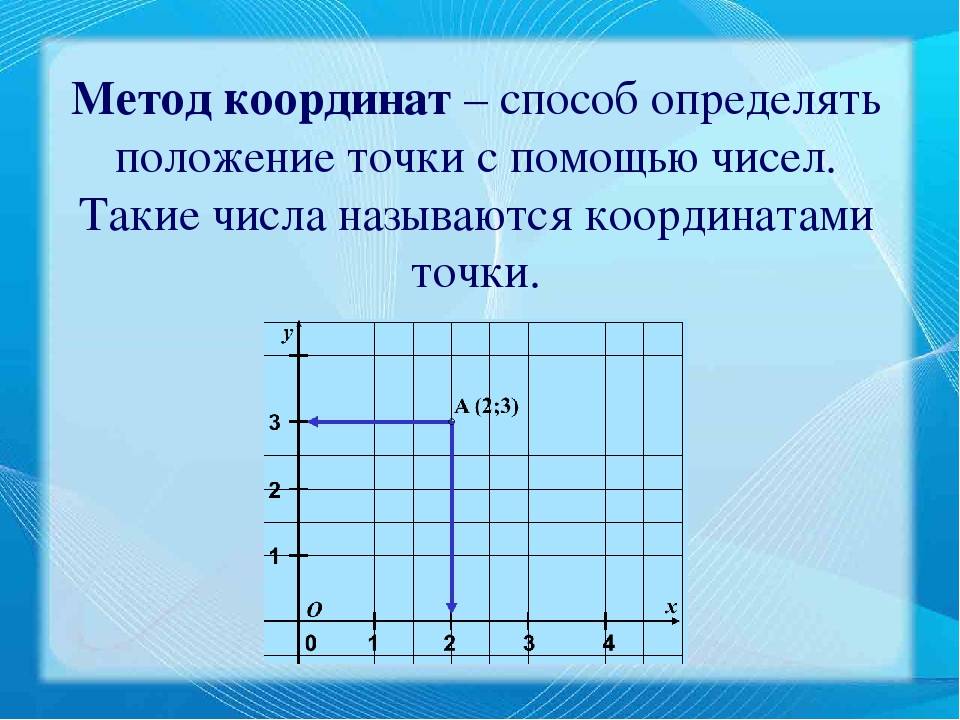
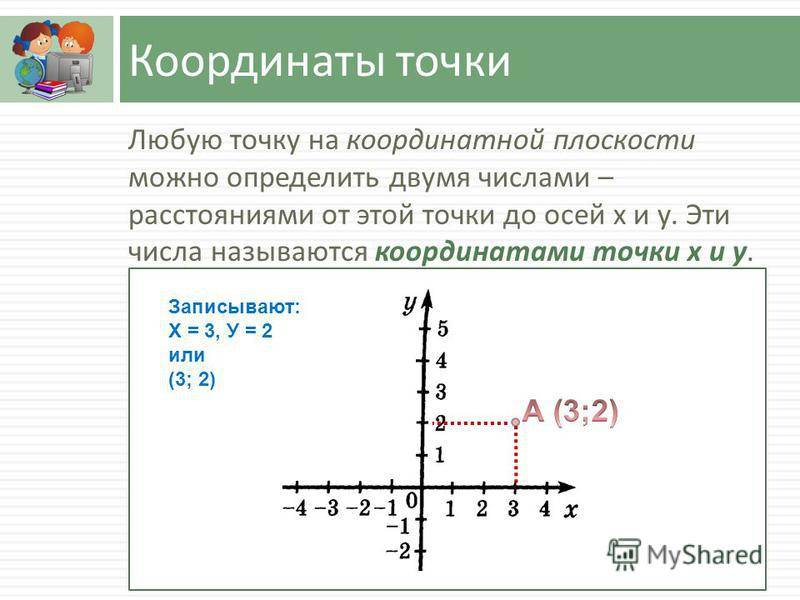
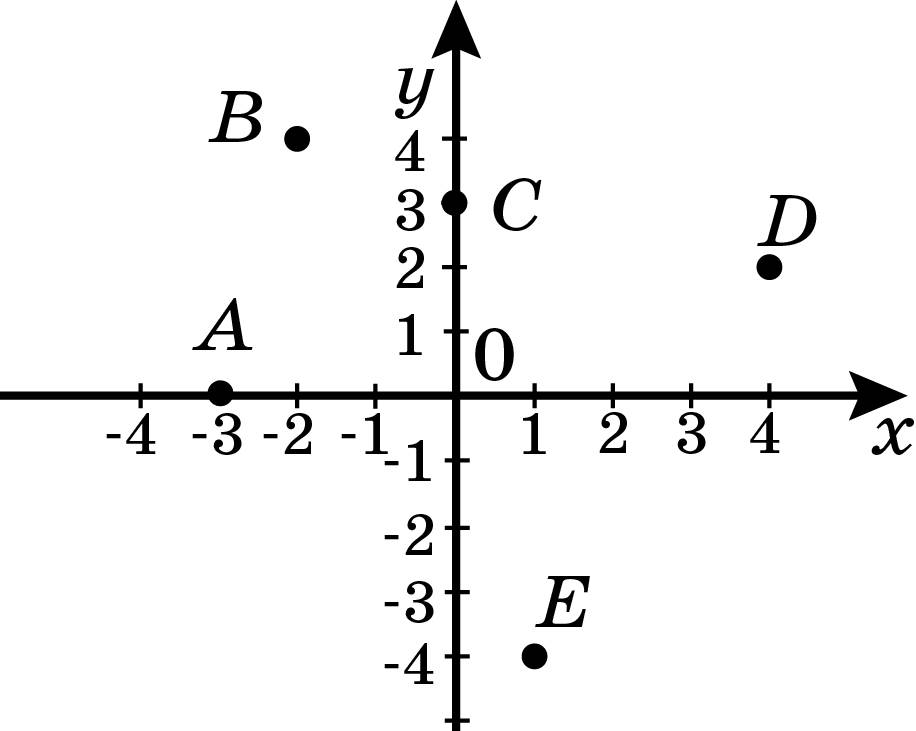
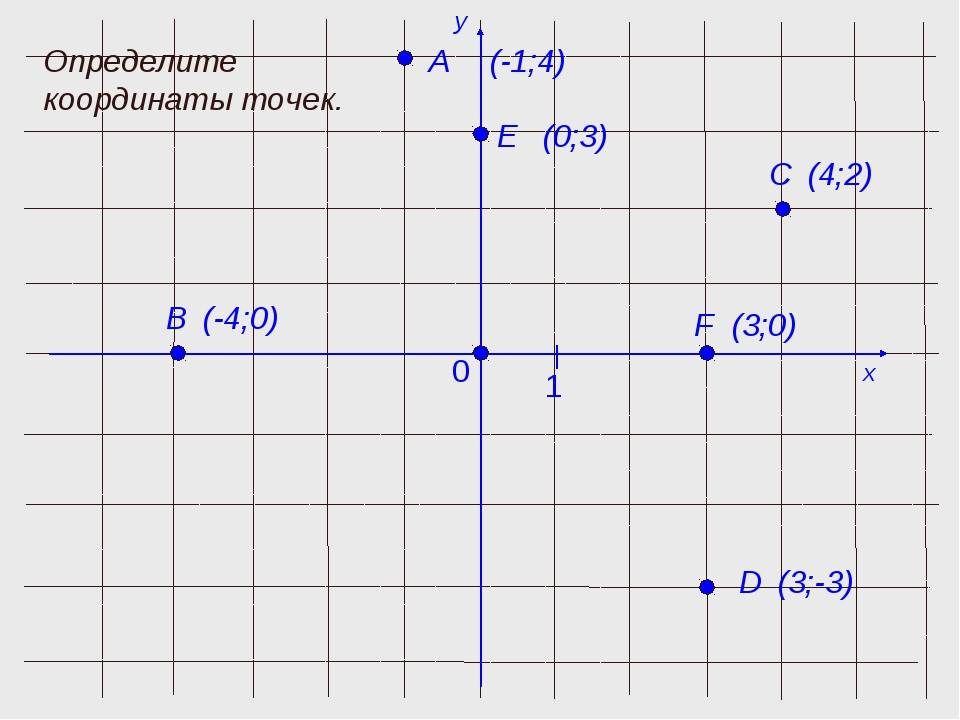
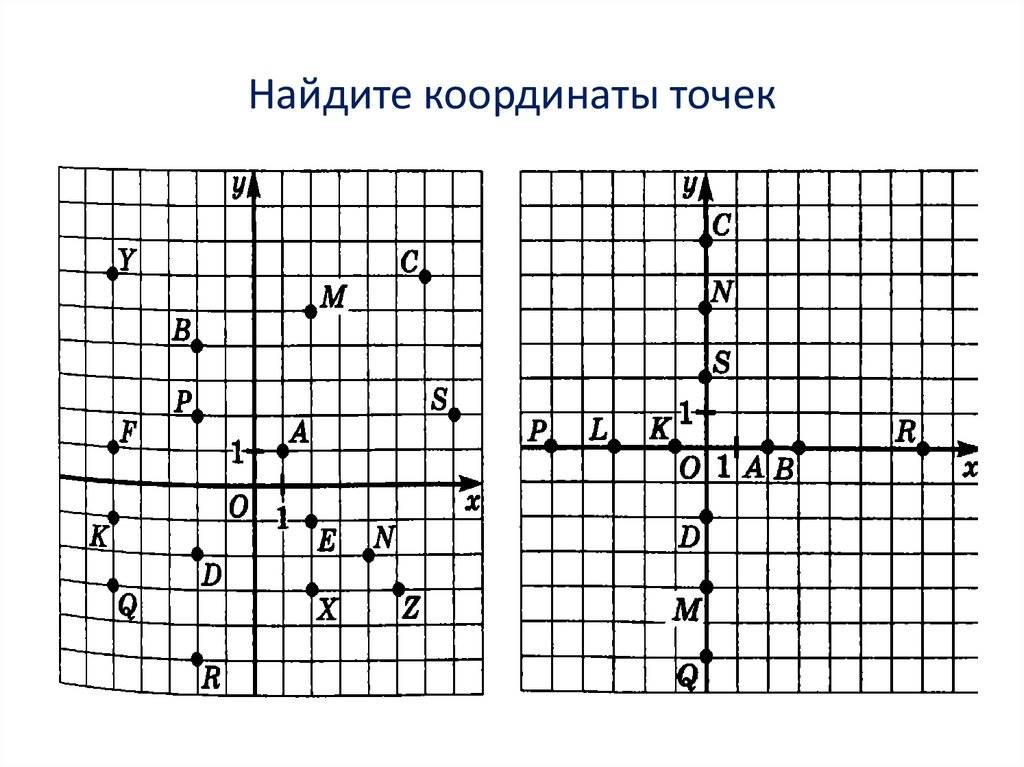
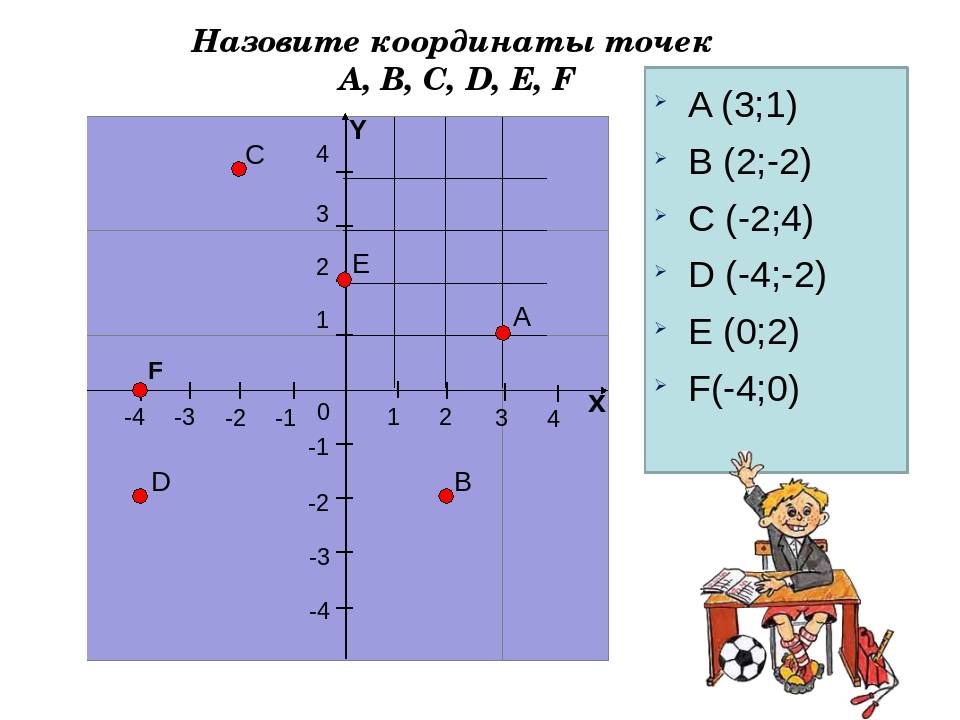
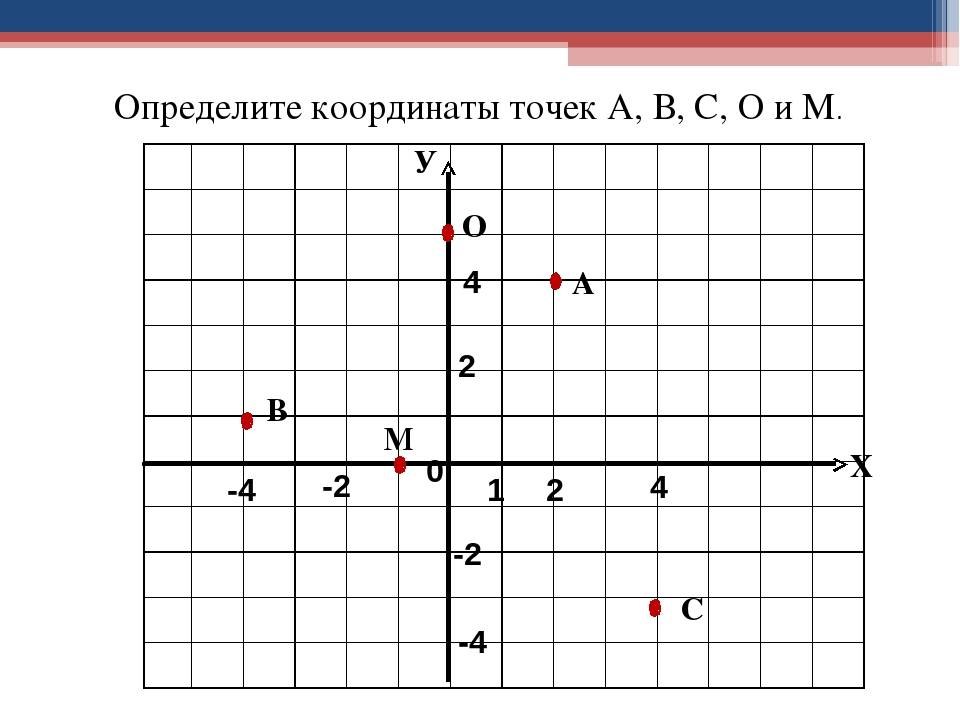
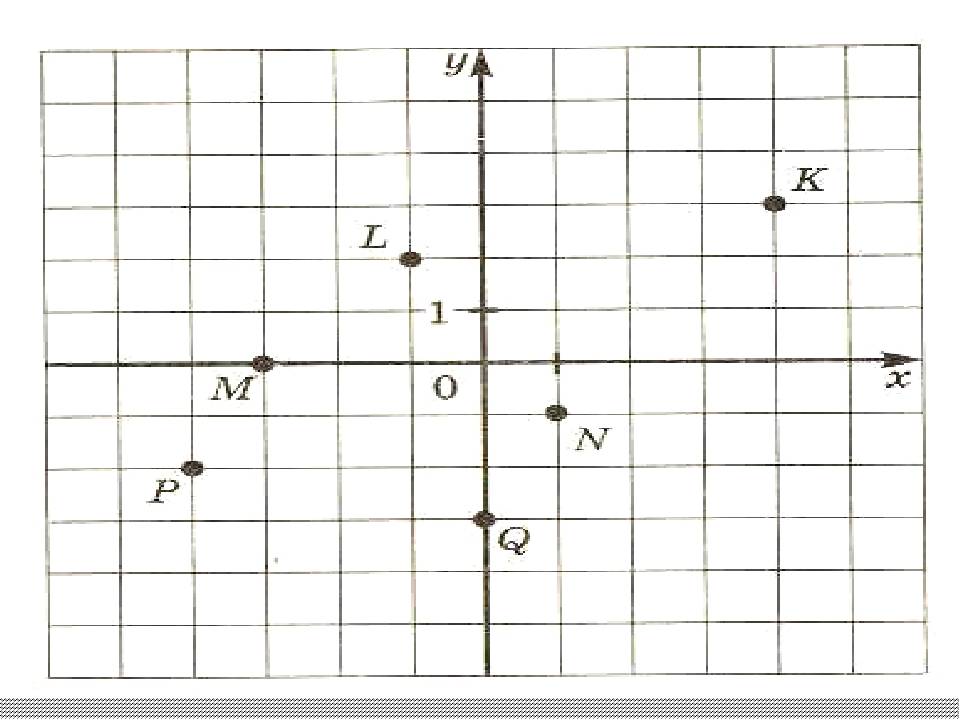
Пусть в плоскости Axy находится произвольная точка. Проведя с неё перпендикуляры на оси, получим два пересечения. Числовые значения в этих местах и будут определять положение A на плоскости, то есть её координаты. Записывают их как A (x, y) и называют декартовыми. Таким образом, нахождение A сводится к определению двух точек, лежащих на осях x и y.

Когда точка располагается на оси X, то её ордината имеет нулевое значение, а если Y — абсцисса. В зависимости от того, в какой четверти находится исследуемый объект, определяется знак его координат. В первой оба числа положительные, а в третьей — отрицательные. Во второй же абсцисса имеет положительное значение, а ордината — отрицательное. В третьей же знаки координат обратные второй четверти.

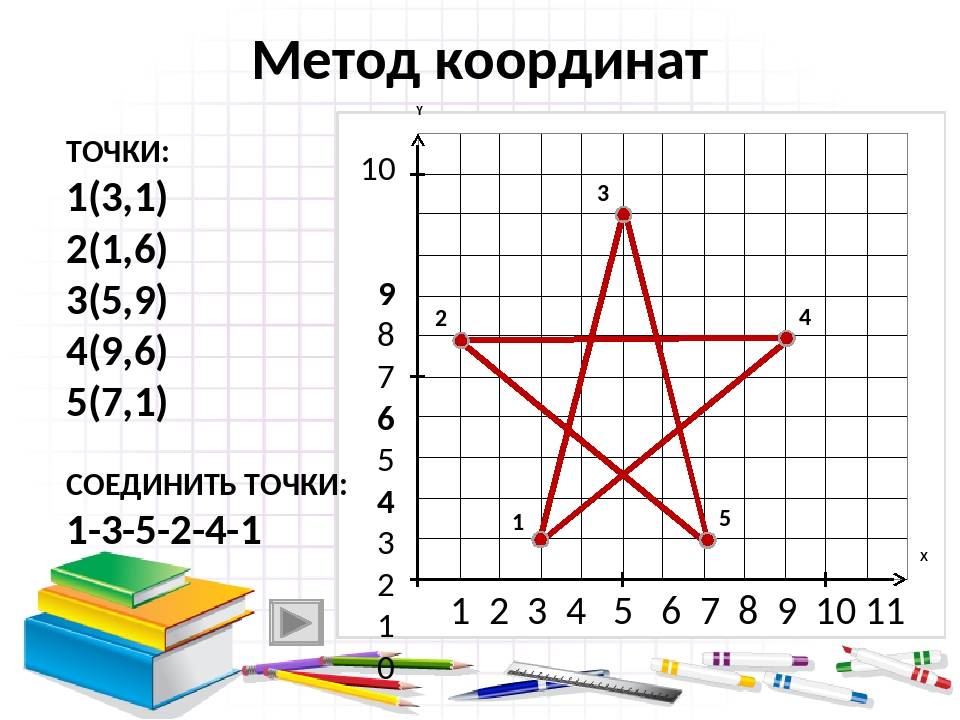
Естественно, что каждой точке на плоскости соответствует пара чисел. Любая фигура состоит из множества точек. Проведя учёт точек и зная их взаимоотношение относительно друг друга, можно изучить свойство объекта. Эти вычисления позволяет выполнить алгебра и арифметика. Поэтому появляется возможность решать геометрические задачи наглядными алгебраическими способами.

В этом и лежит основа использования метода координат в пространстве. Формулы, применяемые при расчётах, хотя и выглядят устрашающе, на самом деле запоминаются легко. Правда, для этого следует выполнить несколько практических заданий.

Координаты на прямой

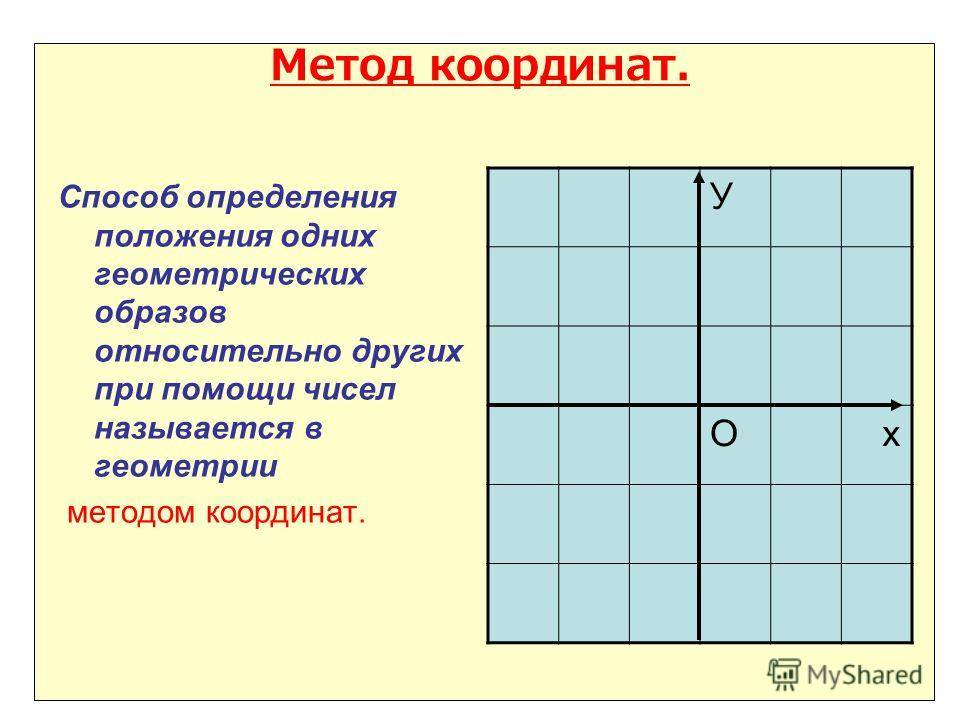
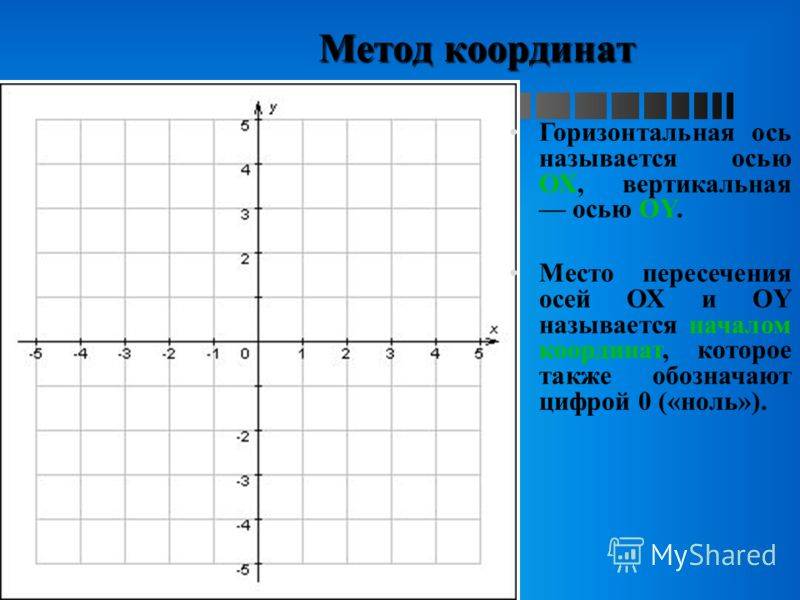
Исследование свойств геометрических тел привело к возникновению отдельной науки — аналитической геометрии. Основополагающим открытием, позволяющим решать задачи, связанные с фигурами, стал координатный метод. В математике принято под координатами понимать положение точки на линии, поверхности или пространстве.

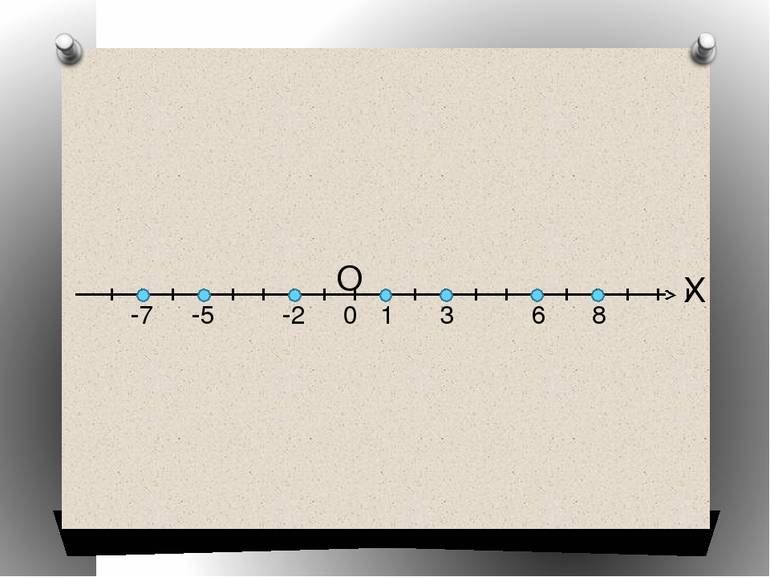
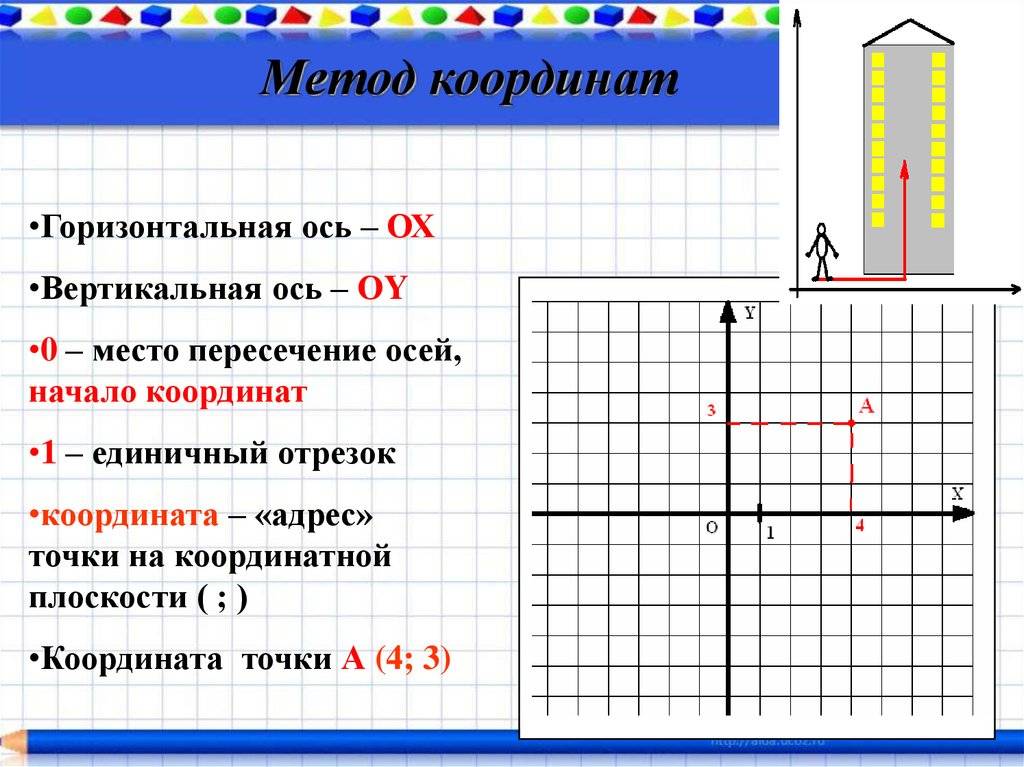
Самая элементарная задача, дающая возможность разобраться в сути, связана с определением положения точки на прямой. Пусть на линии указаны две произвольные точки A и B. Отрезок, который они ограничивают, принимают за единицу длины. Каждой точке P, входящей в AB, соответствует величина, называемая координатой.

Принимать она может три значения:

1. Положительное. Если P находится на отрезке AP и лежит по ту же сторону от A, что и точка B.
2. Отрицательное. Если P принадлежит отрезку AP, но при этом точки P и B находятся по разные стороны от B.
3. Нулевое. Значение координаты точки A равняется нулю.

При выполнении этих условий отрезок называют числовой осью, а A — началом координат. Любая точка, располагающаяся на прямой, имеет свою координату, отличную от других. Но при этом каждое действительное число указывает на расположение точки на рассматриваемой числовой оси. Например, запись вида A (2), B (-¾) обозначает, что числа в скобках являются координатами соответствующих точек.

Основные формулы

Зачастую в задачах, касающихся расчёта фигур, необходимо посчитать величину отрезка, лежащего на плоскости. Например, это может быть высота, медиана, биссектриса, радиус или сторона. Основной формулой считается выражение, позволяющее найти расстояние между двумя точками. Если даны две координаты A (x1, y1) и B (x2, y2), то искомое значение определяется по формуле: P (A, B) = ((x2-x1)2 + (y2-y1)2)½.

Если же начало отрезка лежит в нулевой точке, то выражение для вычисления его длины упрощается до вида: P (A, B) = ((x) 2 + (y)2)½, то есть нахождения суммы квадратов чисел, определяющих координаты. Фактически это теорема Пифагора, изучаемая в шестом классе общеобразовательной школы.

Кроме нахождения длины отрезка, к основным формулам относят:

1. Деление отрезков в заданном отношении. Координату C (xc, yc), образованную из A (x1, y1) и B (x2, y2), определяют из соотношения: AC/CB = α1/α2, где α1,2 — действительные числа. Исходя из этого, Xc = (x1α2 + x2α1) / (α1 + α2), Yc = (y1α2 + y2α1) / (α1 + α2). В основе этих формул используется теорема Фалеса.
2. Вычисление угла между векторами. Если есть три точки на плоскости A (x1, y1), B (x2, y2), C (x3, y3), то угол между векторами находится как скалярное произведение, делённое на произведение их длин: cosγ = <AB, AC> / |AB| * |AC|. Таким образом, если вектор AB = (x2-x1), (y2-y1), а AC (x3-x1, y3-y1), то C = ((x2-x1) * (x3-x1) + (y2-y1) * (y3-y1)) / ((x2-x1)2 + (y2-y1)2) * ((x3-x1)2 + (y3-y1)2)½.
3. Уравнение прямой. Для его составления нужна координата точки. Фиксирование положения в пространстве задаётся вектором α, которому рассматриваемая прямая перпендикулярна. Задача, по сути, сводится к написанию уравнения прямой, проходящей через точку N0 (x0, y0), перпендикулярную вектору n (A, B). Формула, удовлетворяющая заданию, имеет вид: A (x-x0) + B (y-y0) = 0. Равенство для прямой, проходящей параллельно вектору, пишется как (x-x0)/a = (y-y0)b. Уравнение же, описывающее прямую, проходящую через две точки, имеет вид: (x-x1)/(x2-x1) = (y-y1)/(y2-y1).

4. Расстояние от точки до прямой. Если имеется точка (x0, y0) и уравнение: Ax+By+C, то расстояние находится из выражения: |Ax0+Byo+C| / (A2+B2)½.

Вычисление площади и высоты

Рассмотрим типовую задачу, встречающуюся в экзаменационных работах. Даны точки с ординатами A (-2, -3); B (-3,4); C (4,5). Необходимо выполнить построение фигуры, найти её площадь и доказать, что угол A равный C.

Если отложить данные точки на плоскости и соединить их, то получится треугольник. Взяв за тождество, что углы A и C равны, можно сделать предположение о равнобедренности треугольника. Это значит, что две его стороны имеют одинаковую длину. Длина стороны AB — это отрезок A и B с заданными координатами. Поэтому равна она будет следующему выражению: AB = ((-2 + 3)2 + (-3 — 4)2)½ = (1 +49)½ = (50)½. По аналогии находится длина другой стороны: BC = ((-3 — 4)2 + (4 — 5)2)½ = 2 = (1 +49)½ = (50)½.

Для того чтобы найти площадь треугольника, используется правило, что она находится умножением высоты на длину стороны, к которой проведена, и делением полученного результата на два: S = h*a/2 = BH * AC /2, где H — точка пересечения высоты и основания.

В равнобедренном треугольнике высота является биссектрисой и медианой, поэтому H лежит на середине отрезка AC. Чтобы найти её положение, используют формулу нахождения координат середины отрезка: H (x, y): X = (-2+4) /2 = 1, Y = (-3+5) / 2 = 1. Искомая точка имеет координаты H (1,1).

Высота находится как корень квадратный из двух точек: BH = ((-3−1)2 + (4−1)2)½ = (16+9)½ = 5. Теперь нужно найти основание треугольника AC. Разницы, из какой координаты вычитать другую, нет, так как результат учитывается по модулю. Основание будет равно: AC = ((-2−4)2 + (-3−5)2)½ = (36 + 64)½ = 10. Полученные значения высоты и основания подставляют в формулу нахождения площади и получают, что она равна: S = 5*10/2 = 25. Задача решена.

Особенности занесения сотрудников на доску почета

Порядок занесения работников на доску нужно установить специальным документом. К примеру, в нем могут фигурировать эти положения:

• Фото сотрудников заносится на стенд сроком на месяц/год.
• Общее число работников, занесенных на доску, не может превышать десяти.
• Процедура осуществляется по согласованию с профсоюзом.

Нормативными актами устанавливаются критерии занесения на доску почета. К примеру, это могут быть следующие критерии:

• Стаж работы не меньше 10 лет.
• Наличие трудовых наград.
• Высокие показатели труда (перевыполнение плана, высокая производительность, достижение главных показателей эффективности).
• Отсутствие дисциплинарных взысканий.
• Внедрение новых идей, научных разработок.
• Участие в общественной деятельности.

Наличие соответствия критериям устанавливает специально созванная группа. Основанием для помещения ФИО сотрудника на стенд является приказ руководителя. Форма его законом не регулируется. Документ составляется в свободном виде. Однако в нем должны быть обязательные сведения: основания для нематериального поощрения, указание на сотрудника.

Образец приказа

ООО «Дело и правда»

Приказ №55

г. Новосибирск

22.03.2021 года

О занесении сотрудника на доску почета

В соответствии с локальным положением №99-А

ПРИКАЗЫВАЮ:

1. За высокие производственные показатели и активное участие в общественной деятельности занести на доску почета специалиста по кадрам Малинину О.Л.
2. Ответственность за занесение сотрудника на доску почета возложить на руководителя отдела Громова О.Д.
3. Громову О.Д. запросить у Малининой О.Л. фото размером 10 на 15.
4. Контроль за исполнением настоящего распоряжения оставляю за собой.

Лунный К.К. (подпись)

С приказом ознакомлены:

Громов О.Д. (подпись)
Малинина О.Л. (подпись)

Нахождение угла

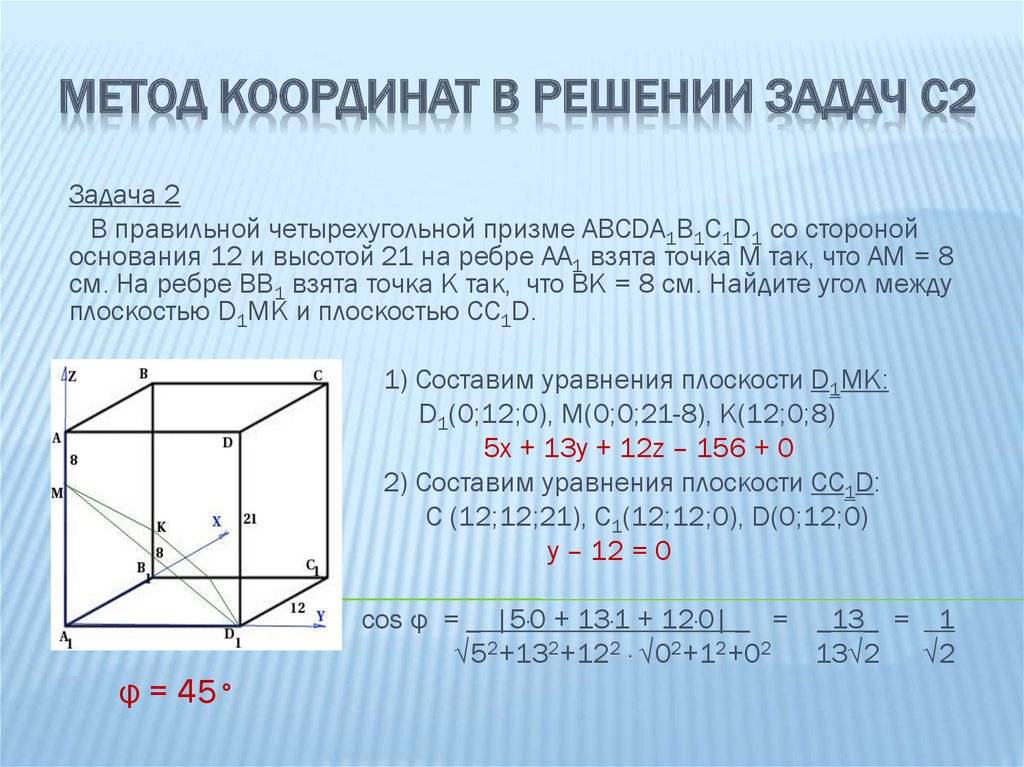
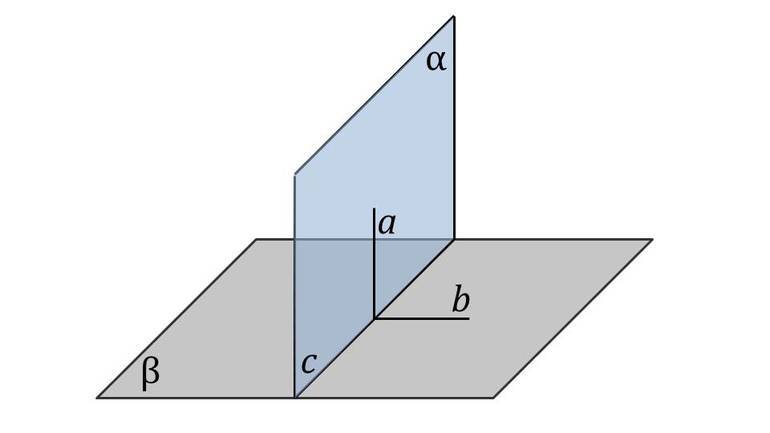
Например, необходимо найти угол между плоскостями. Координатным методом решить поставленную задачу несложно. С точки зрения геометрии, это угол между двумя параллелями. Отметив на поверхности начало координат, через него можно провести перпендикуляры обеим плоскостям. Образованный угол и будет искомым. Поэтому для решения задачи необходимо:

• записать уравнения плоскостей;
• составить векторы нормали;
• вычислить значение косинуса угла между поверхностями.

Для составления уравнений следует найти положение трёх точек, лежащих в плоскости, но не на одной нормали. Затем каждое из них подставить в уравнение и получить систему. Решается последняя любым доступным методом, например, нахождением определителя матрицы или графическим смешанным методом. В итоге находят корни системы A, B, C и составляют вектор нормали. При этом полученные координаты не должны быть коллинеарными, то есть не лежать на одной прямой или быть параллельными.

Пусть имеется единичный куб, в котором нужно найти угол, образованный A1, B1, C1 и C1, D, A1. Вначале определяют координаты первой плоскости и подставляют их в уравнение: Ax+By+Cz+1 = 0. Тут следует отметить: свободный член добавляется из-за того, что поверхности не проходят через середину координат. Точки определяются значениями: A1 (1, 0, 1), B (0,0,1), D (1,1,0). После подстановки система уравнений примет вид:

{A + 0 +C + 1 = 0;

{0 + 0 + C + 1 = 0;

{A + B + 0 + 1 = 0.

Из второго равенства можно определить C. Подставив найденное C в первое равенство, можно выразить A, а после найти B. Таким образом, решением системы будет A = 0, B = -1, C = -1. Вектор нормали, соответственно, будет: N1 (0; -1; -1).

Чтобы составить уравнение второй плоскости, нужно найти координаты лишь С1. Исходя из условия, они будут равны С1 (0; 1; 1), а A и D уже известны. Подставляя данные в уравнение Ax+By+Cz+1 = 0, опять составляют систему и находят её коэффициенты. После решения второй матрицы, например, методом разложения, можно записать координаты второго вектора: N2 (-½; ½; -½).

Теперь, когда известны N1 и N2, нужно найти косинус между ними, являющийся углом двух искомых плоскостей. Используя формулу для вычисления угла векторов, можно получить следующее: cosα = |½ + ½| / (2½ * ¾½) = 1 / (6½/2) = 2/6½ = 6½ / 3. Соответственно, угол равен: α = arccos = 6½ / 3.

Основные сведения и формулы для векторов в координатах

Для того, чтобы выполнить задание рассматриваемым способом, нужно не только сделать чертеж координатной плоскости, но и использовать определенные формулы:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

1. Угол между прямой и плоскостью.
2. Угол между прямыми.
3. Расстояние от точки до плоскости.
4. Угол между плоскостями.
5. Расстояние между скрещивающимися прямыми.
6. Расстояние от точки до прямой.

Угол между прямой и плоскостью

Возьмем первую формулу. Сначала приведем уравнение плоскости, проходящей через три точки:

\(A\left(x_0;y_0;z_0\right),\;B\left(x_1;y_1;z_1\right),\;C\left(x_2;y_2;z_2\right).\)

Уравнение прямой на плоскости выглядит так:

\(Ax+By+C=0\)

Тогда уравнение плоскости в пространстве:

\(Ax+By+Cz+D=0\)

При этом вектор k с координатами (A, B, C) — вектор, перпендикулярный плоскости α. Это называют вектором нормали.

Известно, что три точки в пространстве определяют единственную плоскость. Поэтому если заданы три точки, то мы можем найти уравнение плоскости. Мы можем подставить координаты заданных точек в уравнение плоскости и решить систему из трех уравнений с тремя переменными:

\(\left\{\begin{array}{l}Ax_0+By_0+Cy_0+D=0,\\Ax_1+By_1+Cy_1+D=0,\\Ax_2+By_2+Cy_2+D=0\end{array}\right.\)

В этой системе четыре неизвестных, однако, мы можем избавить от одной, если разделим все на D:

\(\left\{\begin{array}{l}Ax_0+By_0+Cy_0+1=0,\\Ax_1+By_1+Cy_1+1=0,\\Ax_2+By_2+Cy_2+1=0\end{array}\right.\)

После решения этой системы мы найдем коэффициенты уравнения плоскости. 

Угол между прямыми

Она гласит, что прямая АВ имеет направляющий вектор:

\(\overrightarrow{AB}=\{x_1;y_1;z_1\}\)

У прямой CD есть направляющий вектор \(\overrightarrow{СВ}=\{x_2;y_2;z_2\}.\)

\(А \cos\;\left(AB;CD\right)=\frac{\overrightarrow{AB}\times\overrightarrow{CD}}{\left|\overrightarrow{AB}\right|\times\left|\overrightarrow{DC}\right|}=\frac{x_1\times x_2+y_1\times y_2+z_1\times z_2}{\sqrt{x_1^2+y_1^2+z_1^2}\times\sqrt{x_2^2+y_2^2+z_2^2}}.\)

Расстояние от точки до плоскости

Предположим, что даны координаты некоторой точки \(M\left(x_0;y_0;z_0\right)\) и уравнение \(Ax+By+Cz+D=0\). Тогда расстояние от точки до плоскости находят по формуле:

\(d=\frac{Ax_0+By_0+Cz_0+D}{\sqrt{\left(A_2+B_2+C_2\right)}}\). 

Угол между плоскостями

Уравнение первой плоскости:

\(A_1x+B_1y+C_1z+D_1=0\)

второй плоскости:

 \(A_2x+B_2y+C_2z+D_2=0\)

Тогда косинус можно найти по следующей формуле:

\(\cos\;\varphi=\frac{\left|A_1A_2+B_1B_2+C_1C_2\right|}{\sqrt{\left(A_1\right)^2+\left(B_1\right)^2+\left(C_1\right)^2}\times\sqrt{\left(A_2\right)^2+\left(B_2\right)^2+\left(C_2\right)^2}}\)

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми есть расстояние между плоскостью, проходящей через одну из прямых параллельно второй, и второй прямой. Чтобы найти эту величину, необходимо провести прямую b, параллельную с, чтобы с пересекалась с а. Плоскость α, которая проходит через прямые с и а, будет плоскостью, параллельной прямой b. Далее из точки пересечения прямых а и с на прямую b нужно опустить перпендикуляр HB. Затем необходимо найти длину данного отрезка.

Расстояние от точки до прямой

Расстояние от точки до прямой есть длина перпендикуляра, опущенного из точки на прямую.

Уравнение прямой — это \( Ax+By+C=0\)

Тогда можно найти S от точки до прямой с помощью выражения:

\(d=\frac{\left|A\times M_x+B\times M_y+C\right|}{\sqrt{A^2+B^2}}\)

Скалярное произведение

Пусть есть два вектора a и b с известными координатами (x1, y1) и (x2, y2). Формула для выражения скалярного произведения векторов через координаты будет иметь вид: a* b = x1*x2 + y1*y2. То есть это сумма произведений соответствующих координат.

Для доказательства следует отложить два вектора из одной точки, направленные в разные стороны. Соединив их конечные точки, можно утверждать, что полученный вектор будет равняться разности a и b. Для образованного треугольника выполняется теорема косинусов: AB2 = OA2 + OB2 — 2*OA*OB * cosα. Так как AB — это всё равно, что длина вектора по модулю в квадрате, то вместо AB можно написать вектор, равный a-b.

В итоге получится: |a-b| 2 = |a|2 + |b|2 — 2 |a|*|b|*cosα. Последнее перемножение на косинус по определению является скалярным произведением a и b. Выразив его из выражения, справедливо будет записать: a*b = (|a|2 + |b|2 — |a — b|2) /2. Подставив координаты в формулу, получим следующее: a*b = (x12 + y12 + x22 + y22 — (x1-x2)2 + (y1-y2)2) /2 = x1*x2 + y1*y2. Равенство доказано.

Уравнение плоскости

В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой:
$$ A*x+B*y+C*z+D=0,$$
где \(A,B,C,D\) – какие-то числа.

Если найти \(A,B,C,D\), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.

Например, пусть даны три точки:

Подставим координаты точек в общее уравнение плоскости:

Получилась система из трех уравнений, но неизвестных 4: \(A,B,C,D\). Если наша плоскость не проходит через начало координат, то мы можем \(D\) приравнять \(1\), если же проходит, то \(D=0\). Объяснение этому простое: вы можете поделить каждое ваше уравнения на \(D\), от этого уравнение не изменится, но вместо \(D\) будет стоять \(1\), а остальные коэффициенты будут в \(D\) раз меньше.

Теперь у нас есть три уравнения и три неизвестные – можем решить систему:

Пример 3

Найти уравнение плоскости, проходящей через точки
$$ K(1;2;3);\,P(0;1;0);\,L(1;1;1). $$
Подставим координаты точек в уравнение плоскости \(D=1\):
$$\begin{cases} A*1+B*2+C*3+1=0,\\ A*0+B*1+C*0+1=0, \\ A*1+B*1+C*1+1=0.\end{cases}$$
$$\begin{cases} A+2*B+3*C+1=0,\\ B+1=0, \\ A+B+C+1=0.\end{cases}$$
$$\begin{cases} A-2+3*C+1=0,\\ B=-1, \\ A=-C.\end{cases}$$
$$\begin{cases} A=-0.5,\\ B=-1, \\ C=0.5.\end{cases}$$
Получаем искомое уравнение плоскости:
$$ -0.5x-y+0.5z+1=0.$$