Рекурсивное решение для доски произвольного размера на C++[]
Вариант решения на C++
// Backtracking method. "Поиск с возвратом" на примере
// задачи о восьми ферзях.
#include <iostream>
const int SIZE = 8; // Размер.
int boardSIZE];
int results_count = ; // Количество решений.
// Функция showBoard() - отображает доску.
void showBoard()
{
for(int a = ; a < SIZE; ++a)
{
for(int b = ; b < SIZE; ++b)
{
std::cout << ((boarda]) ? "Q " ". ");
}
std::cout << '\n';
}
}
// Функция tryQueen() - проверяет нет ли уже установленных ферзей,
// по вертикали, диагоналям.
bool tryQueen(int a, int b)
{
for(int i = ; i < a; ++i)
{
if(boardi])
{
return false;
}
}
for(int i = 1; i <= a && b-i >= ; ++i)
{
if(boarda-i])
{
return false;
}
}
for(int i = 1; i <= a && b+i < SIZE; i++)
{
if(boarda-i])
{
return false;
}
}
return true;
}
// Функция setQueen() - пробует найти результаты решений.
void setQueen(int a) // a - номер очередной строки в которую нужно поставить очередного ферзя.
{
if(a == SIZE)
{
showBoard();
std::cout << "Result #" << ++results_count << "\n\n";
return; // Опционально.
}
for(int i = ; i < SIZE; ++i)
{
// Здесь проверяем, что если поставим в board ферзя (единицу),
// то он будет единственным в этой строке, столбце и диагоналях.
if(tryQueen(a, i))
{
boarda][i = ;
}
}
return; // Опционально.
}
int main()
{
setQueen();
return ;
}
Альтернативный подход[]
Если решать более общую задачу об N ферзях при помощи описанного выше алгоритма, то такой перебор вариантов даже с использованием описанных выше сокращений будет весьма долго работать уже при N = 20, так как 20! = 2.433Шаблон:E. Поэтому представляет особенный интерес следующий эвристический алгоритм, решающий задачу об N ферзях на поле размером N x N. Он работает для всех N ≥ 4 или N = 1:
- Разделить N на 12 и запомнить остаток (N будет равно 8 для задачи о восьми ферзях).
- Занести в список все четные числа от 2 до N по порядку.
- Если остаток равен 3 или 9, перенести 2 в конец списка.
- Добавить в список все нечетные числа от 1 до N по порядку, но, если остаток равен 8, перевернуть пары соседних чисел (например: 3, 1, 7, 5, 11, 9, …).
- Если остаток равен 2 и N ≥ 3, поменять местами 1 и 3, затем, если N ≥ 5, перенести 5 в конец списка.
- Если остаток равен 3 или 9, переместить 1 и 3 (именно в этом порядке, а не в котором они сейчас) в конец списка.
- Разместить ферзя в первом столбце и в строке с номером, равным первому элементу списка, затем поместить следующего ферзя во втором столбце и в строке с номером, равным второму элементу списка, и т. д.
Для N = 8 результат работы этого алгоритма показан на картинке.
| a | b | c | d | e | f | g | h | ||
| 8 | 8 | ||||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h |
Решение, полученное с помощью эвристики.(5)
Ещё несколько примеров:
- 14 ферзей (остаток 2): 2, 4, 6, 8, 10, 12, 14, 3, 1, 7, 9, 11, 13, 5.
- 15 ферзей (остаток 3): 4, 6, 8, 10, 12, 14, 2, 5, 7, 9, 11, 13, 15, 1, 3.
- 20 ферзей (остаток 8): 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 3, 1, 7, 5, 11, 9, 15, 13, 19, 17.
Реализация на C++
Реализация на C++
#include <iostream>
#include <vector>
#include <algorithm>
int main()
{
int N, Mod;
std::vector < int > L;
std::cin >> N;
Mod = N % 12;
for ( int x = 2; x <= N; x += 2 )
L.push_back( x );
if ( Mod == 3 || Mod == 9 )
{
L.push_back( 2 );
L.erase( L.begin() );
}
if ( Mod == 8 )
{
std::vector < int > V;
for ( int x = 1; x <= N; x += 2 )
V.push_back( x );
for ( int i = 1; i < V.size(); i += 2 )
std::swap( V.at( i ), V.at( i - 1 ) );
for ( int i = ; i < V.size(); ++i )
L.push_back( V.at( i ) );
}
else
for ( int x = 1; x <= N; x += 2 )
L.push_back( x );
if ( Mod == 2 && N >= 3 )
{
std::swap( *std::find( L.begin(), L.end(), 1 ), *std::find( L.begin(), L.end(), 3 ) );
if ( N >= 5 )
{
L.erase( std::find( L.begin(), L.end(), 5 ) );
L.push_back( 5 );
}
}
if ( Mod == 3 || Mod == 9 )
{
L.erase( std::find( L.begin(), L.end(), 1 ) );
L.push_back( 1 );
L.erase( std::find( L.begin(), L.end(), 3 ) );
L.push_back( 3 );
}
for ( int i = ; i < L.size(); ++i )
std::cout << L.at( i ) << " ";
return ;
}
Реализация на Haskell
Реализация на Haskell
position n = evenPosition ++ oddPosition where
modN = n `mod` 12
evenPosition
| modN == 3 || modN == 9 = 4,6..n ++ 2
| otherwise = 2,4..n
oddPosition = oneThree $ fiveSeven others where
others
| modN == 8 = swapPairs 9,11..n
| otherwise = 9,11..n
where
swapPairs [] = []
swapPairs x = x
swapPairs (yxxs) = xyswapPairs xs
fiveSeven
| modN == 2 && n >= 5 = ()
| modN == 8 = ()
| modN == 8 || (modN == 2 && n >= 3) = (,
-- ,
-- ,
-- ]
Реализация на Erlang
Реализация на Erlang
-module(queens).
-export().
pmut([])->
];
pmut(A) ->
)].
start() ->
N = 8, % size of board / num of queens (N>=4)
ListP = pmut(listsseq(1,N)),
Q || Q <- ListP, length(listsusort()) == N,
length(listsusort()) == N
---
$ erl
Erlang R16B03 (erts-5.10.4) source 64-bit smp44 async-threads10 hipe kernel-pollfalse
Eshell V5.10.4 (abort with ^G)
1> queensstart().
,
1,6,8,3,7,4,2,5],
1,7,4,6,8,2,5,3],
1,7,5,8,2,4,6,3],
2,4,6,8,3,1,7,5],
2,5,7,1,3,8,6,4],
2,5,7,4,1,8,6,3],
2,6,1,7,4,8,3,5],
2,6,8,3,1,4,7,5],
2,7,3,6,8,5,1,4],
2,7,5,8,1,4,6,3],
2,8,6,1,3,5,7,4],
3,1,7,5,8,2,4,6],
3,5,2,8,1,7,4,6],
3,5,2,8,6,4,7,1],
3,5,7,1,4,2,8,6],
3,5,8,4,1,7,2,6],
3,6,2,5,8,1,7,4],
3,6,2,7,1,4,8,5],
3,6,2,7,5,1,8,4],
3,6,4,1,8,5,7,2],
3,6,4,2,8,5,7|...],
3,6,8,1,4,7|...],
3,6,8,1,5|...],
3,6,8,2|...],
3,7,2|...],
3,7|...],
3|...],
|...]
Еще один взгляд на проблему «жизнь без последовательностей». Часть вторая (практическая) Промо
В [1 – http://infostart.ru/public/62938/] был предложен метод корректировки списаний по партиям при изменении документов задним числом. Использование данного метода позволяет контролировать остатки при неоперативном проведении и поддерживать учет по партиям всегда в актуальном состоянии, то есть обходиться без механизма последовательности документов. Собственно метод заключался в решении задачи правильного списания по партиям как задачи линейного программирования.
В доказательство работоспособности метода приводится следующая «каркасная» конфигурация «Полигон», в которой этот метод реализован.
1 стартмани
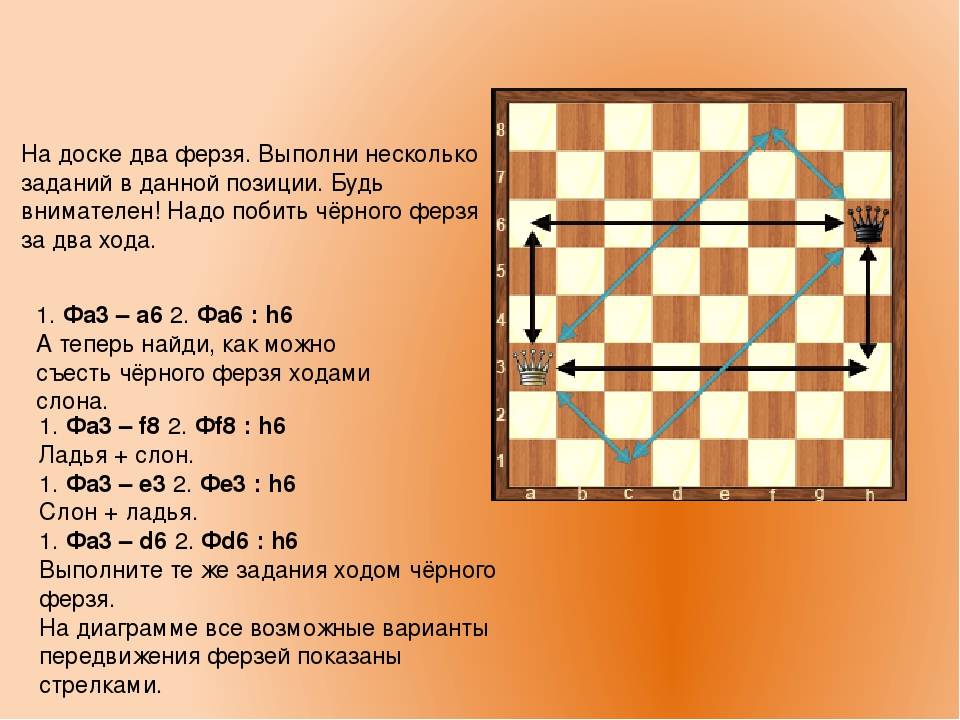
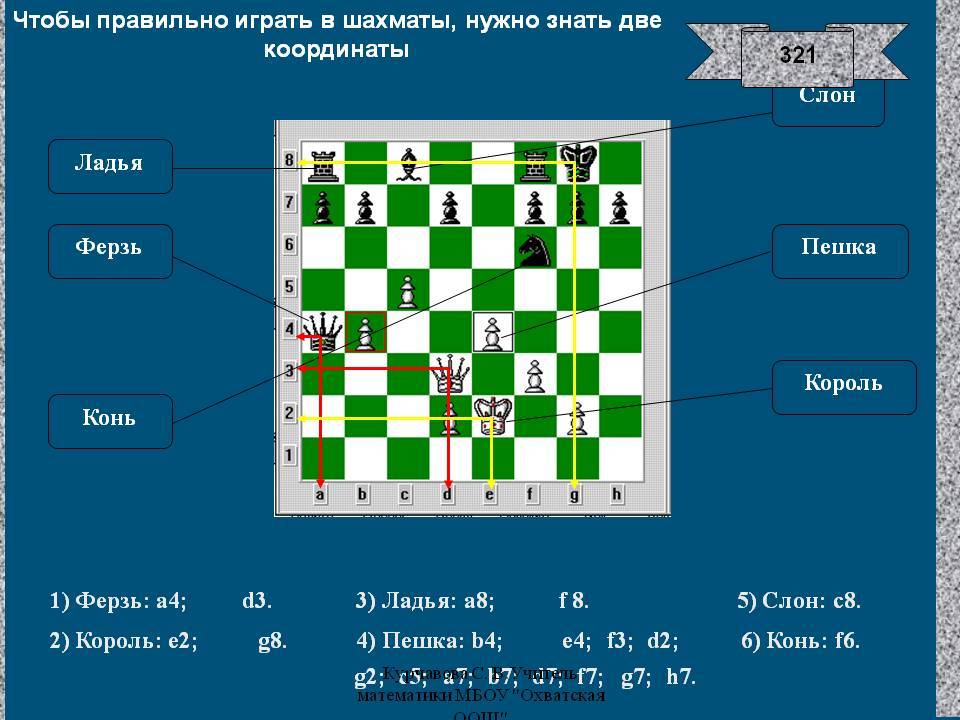
Местоположение на доске и разновидности комбинаций в шахматах
В процессе игры пешки могут по-разному расположиться на доске, несмотря на ограниченность своих возможностей. Опытные игроки в зависимости от местоположения называют фигуры:
- изолированными или блокированными;
- сдвоенными;
- отсталыми;
- проходными
- связанными;
- разрозненными.
От этого зависит выбор тактики, определение роли пешки в дальнейшей игре, выбор ходов.
Данные фигуры обычно начинают сражение, редко когда игроки право первого хода отдают коню. Самым распространенным вариантом является выход пешки, стоящей на позиции е2 на 2 поля вперед, есть несколько классических дебютов, начинающихся с такого хода.
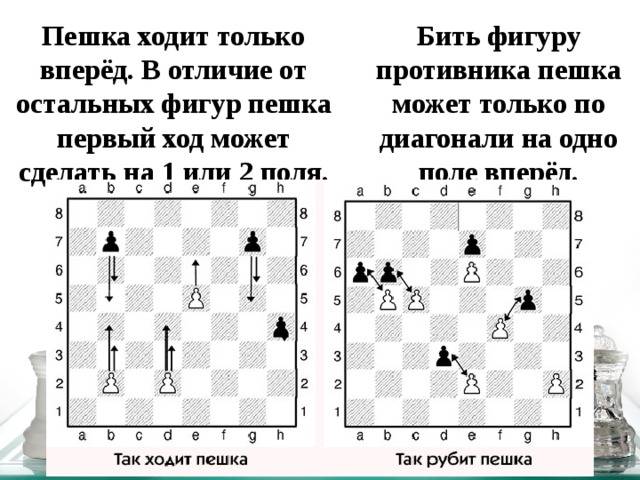
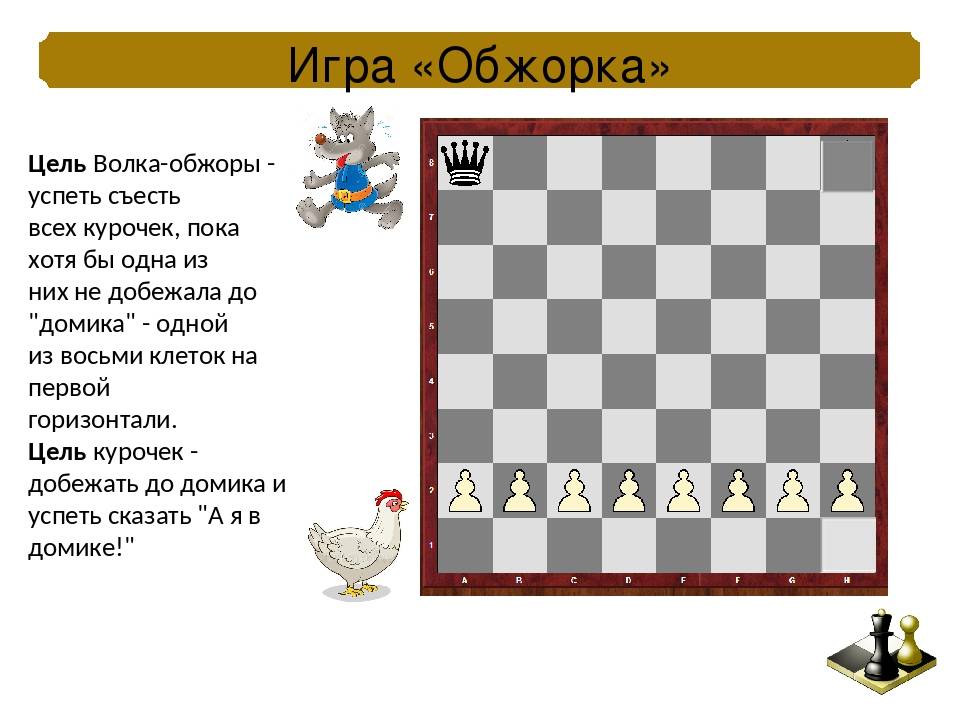
Правила ходов пешками
Перед игрой восемь пешек устанавливаются в ряд на второй горизонтали перед крупными фигурами. Для белых шахмат это полоса под номером 2, для черных №7. Эти фигуры считаются незначительными, являются солдатами армии, которые выполняют мелкие задачи, нередко ими жертвуют для более важных целей. Однако умалять их роль не стоит, в некоторых случаях пешки могут переломить ход игры.
Правила перемещения у пешек простые, они ходят только на одну клетку вперед. Рубит противника пешка только по диагонали, фигуру, стоящую впереди, она «съесть» не может. Есть еще одно исключение. При первом ходе из первоначально выстроенного ряда пешку можно передвинуть вперед сразу на две клетки.
Все шахматные фигуры выполняют две важных задачи. Они обеспечивают защиту королю, предотвращая «пат» и «мат», стараются сбить как можно больше противников.
У пешки есть еще одна немаловажная цель – ей нужно дойти до противоположного края доски. Сделать это крайне сложно, так как на пути у нее очень много шансов быть «съеденной». К тому же этой фигурой часто жертвуют для защиты более важных единиц. Однако если такую задачу удастся выполнить, с пешкой происходит чудесное превращение, она может стать любой другой фигурой, нужной игроку в данный момент. В большинстве случаев она благополучно преобразуется в могущественную королеву. Но это необязательно, игрок может сделать выбор в пользу коня, туры или слона, если для победы ему нужны эти фигуры.
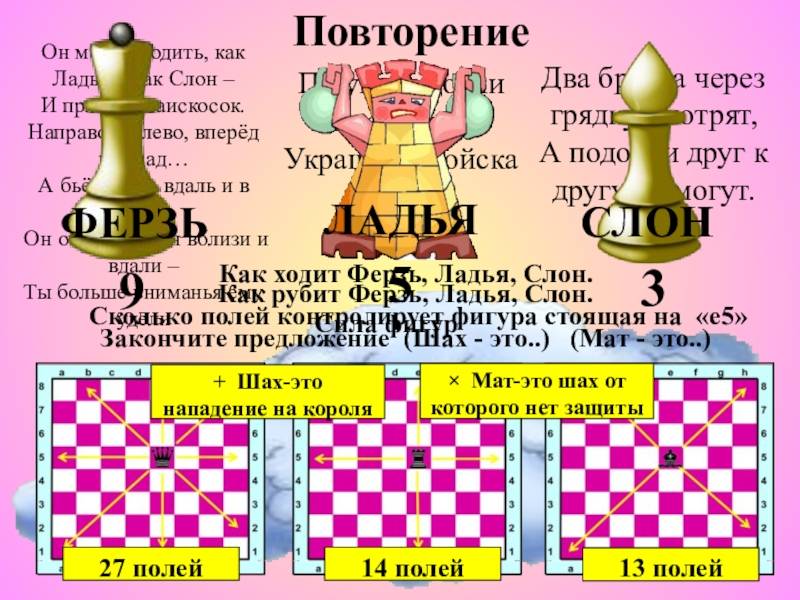
Как расставить шахматы на доске
В углу армии (на клетках а1 и h1 у белых, a8 и h8 у черных) стоят сторожевые башни — ладьи. В русском языке слово «ладья» связано со словом «лодка» и обозначает боевой корабль. А вот в восточных странах ладью называли «рух» по названию хищной птицы (кстати, в английском языке ладья до сих пор называется rook). Изображение ладьи на диаграммах похоже на башню с крепостной стеной ♖.
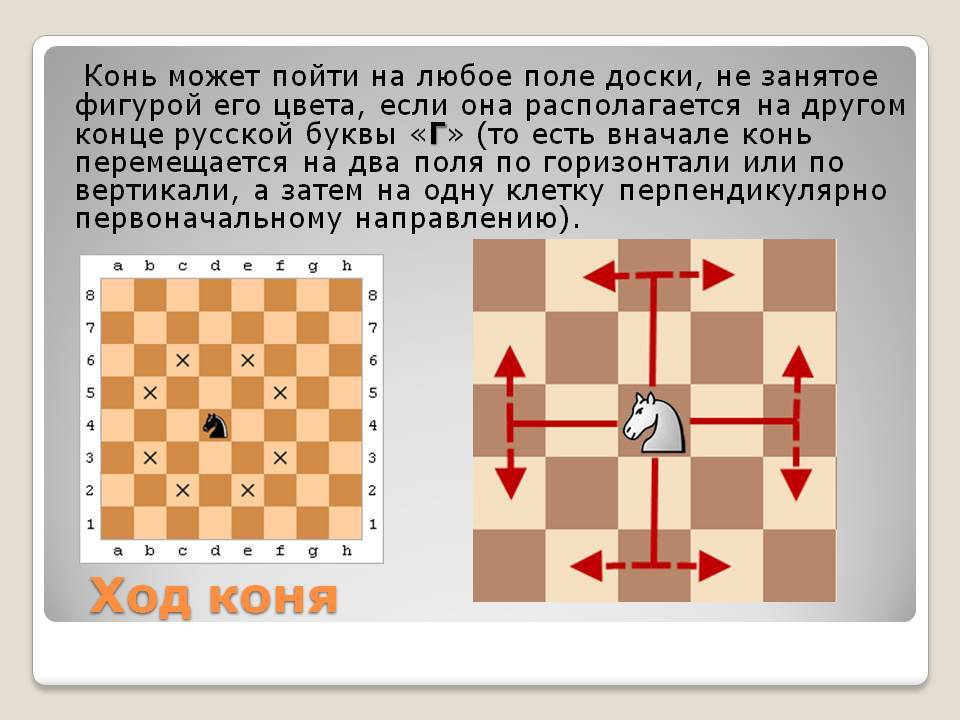
Сбоку от ладей находится шахматный зоопарк, в котором живут кони и слоны. Кони в начале игры стоят на соседней клетке с ладьями (b1 и g1 у белых, b8 и g8 у черных). Шахматного коня ни с кем не спутать — его изображение действительно очень похоже на коня: ♘ . В английском языке конь обозначается словом knight, что переводится как «рыцарь». И правда, раньше эту фигуру часто изображали в виде рыцаря, сидящего верхом на коне.
Рядом с конями, ближе к центру первого и восьмого ряда (с1 и f1 у белых, c8 и f8 у черных), живут шахматные слоны. Шахматы были придуманы в Индии, поэтому неудивительно, что одна из фигур получила такое название — слоны в Индии являются священными животными, которые спокойно ходят по улицам индийских городов. В первых шахматах, подобно коню, эта фигура имела вид всадника, сидящего верхом на слоне. Когда игра пришла в Европу, от слона остался один всадник — у современного шахматного слона нет ни хобота, ни ушей, но название «слон» по традиции осталось. На Руси слона часто называют «офицер», и действительно, у изображения слона на диаграммах обычно рисуют крестик, похожий на орден: ♗ . Но на самом деле этот крестик связан с английским языком: в англоязычных странах слона называют bishop, что переводится как «священник»
У слонов в начальной расстановке шахмат на доске особо важное место — они стоят рядом с королем и ферзем (королевой)
Ну и наконец, в самом центре шахматной армии стоят главные фигуры — король и ферзь. Король — самая главная фигура в шахматах, изображается в виде короны монарха ♔ . Ферзь — самая сильная фигура, главный советник короля. До сих пор у нас ферзя часто называют королевой — изображается он в виде элегантной женской короны ♕ . А в английском языке эта фигура так и называется queen — «королева». Начинающие шахматисты иногда путают, где на шахматной доске стоит король, а где — ферзь. Но запомнить не трудно: король уступает королеве клетку своего цвета. То есть белый ферзь в начале партии стоит на белой клетке (d1), а черный ферзь — на черной клетке (d8). А королям остаются поля е1 и е8.
Итак, все шахматные фигуры расставлены в нужном порядке на первой и восьмой горизонтали. А перед каждой фигурой в начале партии стоит маленький солдатик — пешка. У каждого игрока в начале партии есть целых восемь пешек, но каждая из них, если дойдет до конца доски, сможет превратиться в любую фигуру. Конечно, обычно пешку превращают в самую сильную фигуру.
1С+Классы. Версия-0
Разработано ООП-расширение языка 1С, включающее (но не ограничивающееся):
Классы как абстрактные типы данных с элементами «переменная», «свойство», «функция», «процедура»; Интерфейсы как абстрактные классы без элементов состояния («переменная») и без привязки к реализации методов (свойств, процедур, функций) при определении; Имплементация (реализация) интерфейсов классами;
– одиночное открытое наследование; Области видимости «внутренняя» (private), «экспорт» (public), «защищенная» (protected); Статические элементы классов (общие для всех экземпляров класса); Замещение (переопределение реализации) методов при наследовании – «виртуальные методы, свойства»; Сокрытие (затенение) обычных (не замещаемых) элементов при наследовании; Перегрузка процедур и функций по количеству и типам данных аргументов; Конструкторы класса; Деструктор класса; Слабые ссылки; Делегаты.
1 стартмани
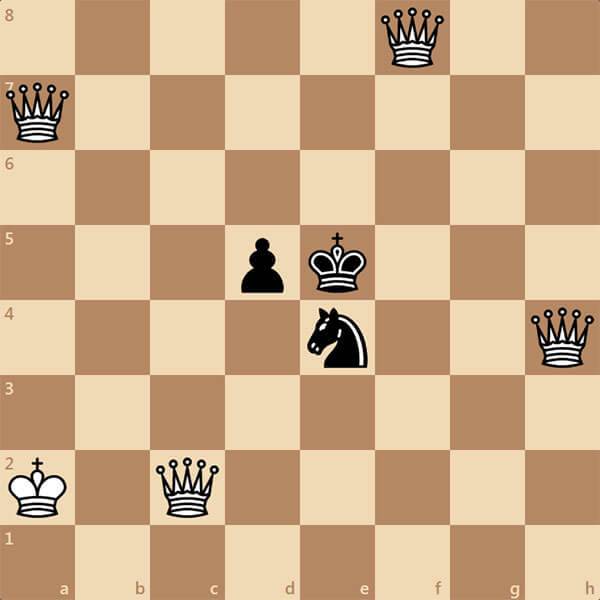
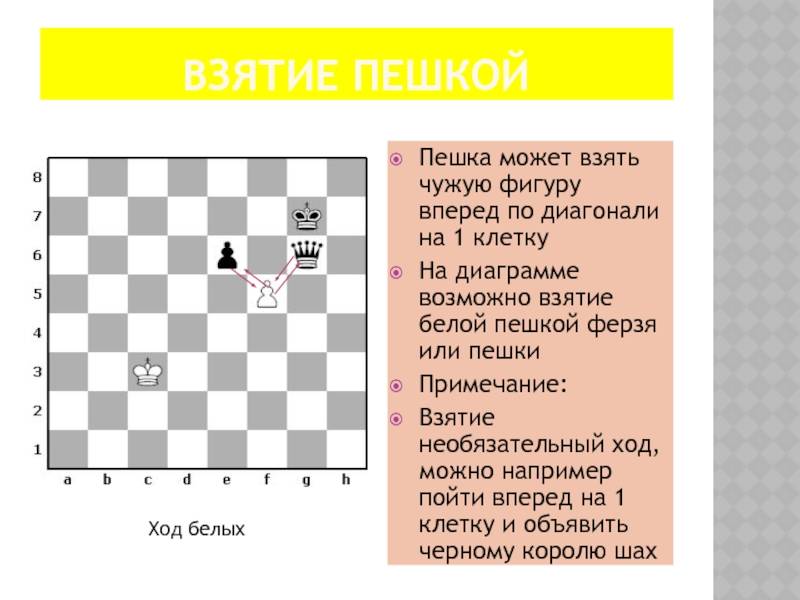
Может ли пешка бить назад?
Есть определенные аналогии между перемещениями пешки и короля. Обе эти фигуры могут делать ход на одно поле, рубить фигуры противника, расположенные по диагонали на соседних клетках. Поэтому у начинающих игроков возникает законный вопрос, может ли пешка есть назад в шахматах. Такой ход существенно расширил бы возможности этой фигуры, позволил бы разблокировать фигуру при встрече двух пешек на вертикали.
Новичкам следует помнить, что для пешек движение назад запрещено, это правило касается и взятия фигур противника. У пешки такой возможности нет, она может ходить только вперед, есть по диагоналям, расположенным перед ней. Если по каким-либо причинам игрок не знал, бьет ли пешка назад, и делает такой ход, по шахматным правилам партия заканчивается. Шахматисту, совершившему ошибку, присуждается проигрыш. Поэтому такое правило необходимо усвоить твердо, не забывать о нем!
Изучив все возможности и ограничения, предусмотренные для пешек, можно реально оценить их роль в шахматной игре. Не нужно недооценивать этих исполнительных «солдат». С их помощью можно решать немало задач и создавать для противника сложные ситуации.
Вариант решения для доски размера до 10-11 на Oracle 11 SQL[]
В Oracle SQL возможно решение одним рекурсивным оператором. Время выполнения — секунды для доски 8*8, до 1 минуты для доски 9*9.
Использован усовершенствованный метод поиска с возвратом:
На доске есть четыре типа ресурсов: вертикали, горизонтали, левые и правые диагонали.
Каждая поставленная фигура на доску «потребляет» одну горизонталь, одну вертикаль, и две диагонали.
Соответственно, следующего ферзя мы будем пробовать ставить на ту клетку, для которого есть оставшиеся незанятые горизонталь, вертикаль и диагонали.
Этим существенно сокращаем время перебора.
Вариант решения на SQL
with
T1 as (select level - 1 as K from dual connect by level <= &&D)
, T2 (N, L, X, Y, D1, D2, NL)
as (select a.K * &D + b.K,
, power (2, a.K), power (2, b.K), power (2, a.K - b.K + &D - 1)
, power (2, a.K + b.K), chr (a.K + 97) || to_char (b.K + 1)
from T1 a, T1 b)
, T3 (RN, RL, RX, RY, RD1, RD2, RNL)
as (select * from T2 union all
select N, RL + 1, RX + X, RY + Y, RD1 + D1, RD2 + D2, RNL || ' ' || NL
from T2, T3
where bitand (RX , X ) = and bitand (RY , Y ) =
and bitand (RD1, D1) = and bitand (RD2, D2) = and N > RN
)
select RNL from T3 where RL = &D - 1;
Общие маты
Помощник по рангу
Из Берджесса, стр. 16
| а | б | c | d | е | ж | грамм | час | ||
| 8 | 8 | ||||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| а | б | c | d | е | ж | грамм | час |
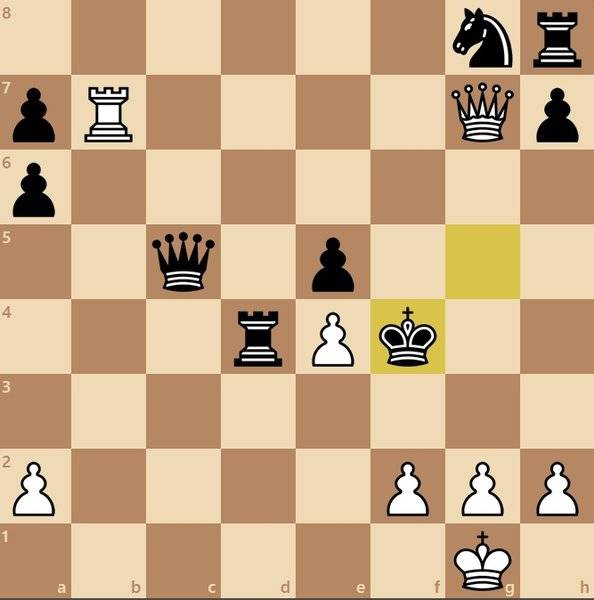
Белые выигрывают ходом 1.Rd8 #.
Мат на заднем ряду – это мат, поставленный ладьей или ферзем на заднем ряду (то есть в ряду, в котором фигуры стоят в начале игры), в котором матовый король не может продвинуться вверх. доска, потому что король заблокирован дружественными фигурами (обычно пешками) на второй горизонтали. На диаграмме показан пример мата на втором месте. Он также известен как помощник по коридору .
Товарищ ученого
Помощник ученого – черным поставлен мат. | Анимация, демонстрирующая помощник ученого |
Мат ученого (также известный как мат с четырьмя ходами) – это мат, достигаемый ходами:
- 1. e4 e5 2. Qh5 Nc6 3. Bc4 Nf6 ?? 4. Фxf7 #
Ходы могут быть сыграны в другом порядке или с небольшими вариациями, но основная идея та же: ферзь и слон объединяются в простой матовой атаке на f7 (или f2, если черные выполняют мат). Есть и другие способы поставить мат в четыре хода.
Приятель дурака
Мат дурака – белым поставлен мат. | Анимация, демонстрирующая друг дурака |
Мат дурака , также известный как «Мат с двумя ходами», является самым быстрым матом из возможных. Яркий пример состоит из ходов:
- 1. f3 e5 2. g4 Qh4 #
приводя к показанному положению. (Схема может иметь небольшие вариации, например, белые могут сыграть f2 – f4 вместо f2 – f3 или сначала пойти пешкой g , а черные могут сыграть … e7 – e6 вместо … e7 – e5.)
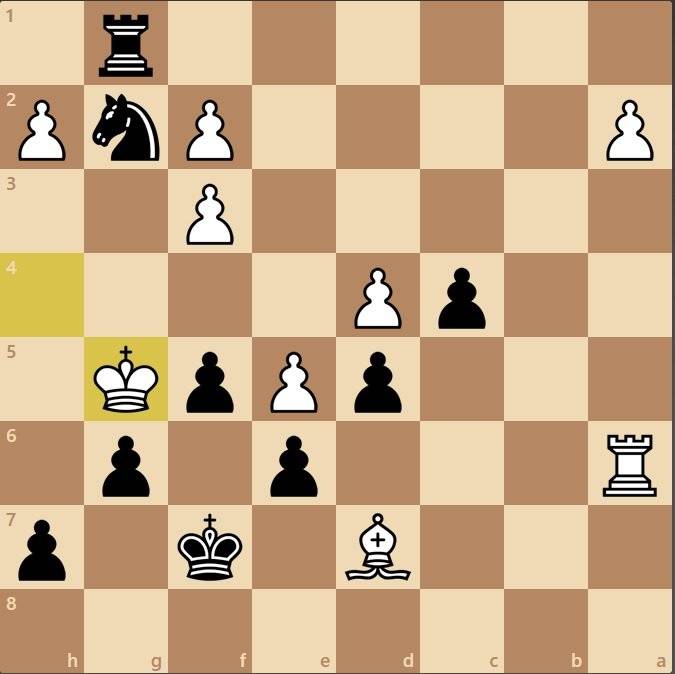
Спертый мат
Задушенный мат после 27.Nf7 + Kg8 28.Nh6 + Kh8 29.Qg8 + Rxg8 30.Nf7 #. |
Конечная позиция |
Спертый мат является мат поставляется в рыцаре , в котором Mated король не в состоянии двигаться , потому что он окружен (или задушен ) своими собственными частями.
Мат обычно виден в углу доски, так как там нужно меньше фигур, чтобы окружить короля. Наиболее часто встречающаяся форма задушенного товарища видна на диаграмме рядом. Рыцарь на f7 поставляет мат королю на h8 , который предотвращен от возможности избежать проверки со стороны ладьи на g8 и пешки на g7 и h7. Точно так же белые могут получить мат с белым королем на h1 и конем на f2. Аналогичные маты на a1 и a8 встречаются реже, потому что рокировка на более распространена, поскольку она безопасно помещает короля ближе к углу по сравнению с рокировкой на фланг.
Вариант решения для доски произвольного размера на C#[]
Ниже приведен только класс, непосредственно реализующий алгоритм решения.
Вариант решения на C#
class QueensProblem IProblem {
private int size;
private int[] positions;
private List<int[]> saved;
private IProblemCallback cb;
public void Init(int size, IProblemCallback cb) {
this.size = size;
this.cb = cb;
positions = new intsize];
saved = new List<int[]>();
}
private void Save() {
saved.Add((int[]) positions.Clone());
}
private bool Step() {
int s = size;
for (int i = 1; i < s; i++) {
int pos = positionsi];
while (true) {
bool found = false;
for (int j = ; j < i; j++) {
int epos = positionsj];
if (epos == pos || pos - i == epos - j || pos + i == epos + j) {
if (++pos >= s) {
if (!Next(i)) return false;
while (++i < s) positionsi = ;
return true;
}
positionsi = pos;
found = true;
break;
}
}
if (!found) break;
}
}
Save();
return Next(s - 1);
}
private bool Next(int pos) {
int s = size;
if (++positionspos < s) return true;
do {
positionspos = ;
if (++positions;
if (part != prev) cb.Progress((float) (prev = part) sq);
}
return saved.Count;
}
public List<int[]> GetResults() {
return saved;
}
public int Size {
get { return size; }
}
}
Время выполнения алгоритма
Файл:Queens time log.png
График зависимости времени от размера (экспоненциальный)
Ниже представлена зависимость времени выполнения программы от размера доски (время приведено для компьютера с процессором Intel Core2 Q6600 @ 2.4 ГГц):
| Размер | Решений | Время (мс) |
|---|---|---|
| 4 | 2 | 1 |
| 5 | 10 | 2 |
| 6 | 4 | 2 |
| 7 | 40 | 2 |
| 8 | 92 | 3 |
| 9 | 352 | 6 |
| 10 | 724 | 16 |
| 11 | 2 680 | 69 |
| 12 | 14 200 | 376 |
| 13 | 73 712 | 2 311 |
| 14 | 365 596 | 15 411 |
| 15 | 2 279 184 | 108 587 |
| 16 | 14 772 512 | 812 945 |
Характер зависимости времени выполнения от размера доски — экспоненциальный (как показано на графике).
Вариант решения для доски произвольного размера на C[]
Здесь приведена программа, решающая задачу для размеров доски от 1 до 17. Программа измеряет и выводит время работы алгоритма.
Вариант решения на C
#include <time.h>
#include <stdio.h>
#include <string.h>
#define SIZE 20
int size,
sol_num,
a SIZE ];
struct _board {
unsigned int a SIZE ];
} board SIZE+1 ];
void dfs(register int ind)
{
register int i, j;
if (ind >= size)
{
++sol_num;
return;
}
for (aind = ; aind < size; ++aind])
{
if (!(boardinda ind & (1<<aind])))
{
memcpy(boardind+1a, &boardinda , SIZE*sizeof(int));
for (i = ind, j = aind]; i<size && j<size; ++i, ++j)
boardind+1ai |= (1<<j);
for (i = ind, j = aind]; i<size && j>=; ++i, --j)
boardind+1ai |= (1<<j);
boardind+1aind = 65535u;
for (i = ind; i < size; ++i)
boardind+1ai |= 1<<aind];
dfs(ind+1);
}
}
}
int main()
{
double start, end;
int i;
for (size = 1; size < 20; ++size)
{
start = clock();
sol_num = ;
memset(a, , sizeof(int)*SIZE);
for (i = ; i < SIZE+1; ++i)
memset(boardia, , sizeof(int)*SIZE);
dfs();
end = clock();
printf("%20d%20d\ttime: %.2lf\n", size, sol_num, (end-start)CLOCKS_PER_SEC);
}
return ;
}
Время выполнения алгоритма
Ниже представлена зависимость времени выполнения программы от размера доски (время приведено для компьютера с процессором Intel Core i5-2410M @ 2.3 ГГц):
| Размер | Решений | Время (с) |
|---|---|---|
| 1 | 1 | 0.000 003 |
| 2 | 0.000 001 | |
| 3 | 0.000 001 | |
| 4 | 2 | 0.000 004 |
| 5 | 10 | 0.000 008 |
| 6 | 4 | 0.000 025 |
| 7 | 40 | 0.000 091 |
| 8 | 92 | 0.000 347 |
| 9 | 352 | 0.001 508 |
| 10 | 724 | 0.008 023 |
| 11 | 2 680 | 0.031 750 |
| 12 | 14 200 | 0.114 120 |
| 13 | 73 712 | 0.538 676 |
| 14 | 365 596 | 3.267 996 |
| 15 | 2 279 184 | 21.486 720 |
| 16 | 14 772 512 | 147.388 255 |
| 17 | 95 815 104 | 1 088.978 601 |
| 18 | 666 090 624 | 8 776.579 792 |
Формулировка[]
В более «математическом» виде задача может быть сформулирована несколькими способами, например, так: «Заполнить матрицу размером 8×8 нулями и единицами таким образом, чтобы сумма всех элементов матрицы была равна 8, при этом сумма элементов ни в одном столбце, строке или диагональном ряде матрицы не превышала единицы».
Конечная цель, поставленная перед решающим задачу, может формулироваться в нескольких вариантах:
- Построить одно, любое решение задачи.
- Аналитически доказать, что решение существует.
- Определить количество решений.
- Построить все возможные решения.
- Одна из типовых задач по программированию алгоритмов перебора: создать компьютерную программу, находящую все возможные решения задачи.
Иногда постановка задачи требует нахождения способов расстановки N ферзей на доске N×N клеток (при этом при 1<N<4 задача не имеет решения).
Мы же подробнее рассмотрим классический “шахматный” случай для доски 8*8.