Составные поверхности. Введение: порции поверхности по Кунсу
Oбсудим ряд методов определения поверхностей. Hекоторые из этих методов
основаны на системе построения двух пересекающихся семейств кривых, поэтому
начнем с рассмотрения процедур этого типа. Допустим, что необходимая сетка
кривых уже построена каким-либо методом. Для большей общности будем сначала
применять параметрическое представление, введя семейства продольных и
трансверсальных кривых; параметры этих кривых обозначим через x и y
соответственно. Потом полученные результаты будут применены и к
непараметрическому случаю.
Сетка кривых делит поверхность на совокупность топологически прямоугольных
порций, каждая из которых ограничена парой u-кривых и парой v-кривых, как
показано на рис. 8.1. Допустим, что u и v изменяются
в пределах от 0 до 1 вдоль соответствующих границ; тогда r(u, v),
0 < u, v < 1, представляет внутренность порции
поверхности, r(u, 0), r(1, v), r(u, 1) и r(0, v) представляют четыре известные
граничные кривые. Тем самым задача определения порции поверхности сводится к
нахождению функции r(u, v) с подходящим типом «хорошего поведения», которая при
u = 0, u = 1, v = 0 или v = 1 представляет нужную граничную кривую.
Рассмотрим сперва более простую задачу построения порции поверхности, если
заданы только две ее границы r(0, v) и r(1, v). Применяя линейную интерполяцию
в u-направлении, получим линейчатую поверхностьr1(u, v) = (1 – u)r(0, v) + ur(1, v) (*).
Напротив, линейная интерполяция в v-направлении дает поверхность,
удовлетворяющую двум другим граничным условиям:r2(u, v) = (1 – v)r(u, 0) – vr(u, 1) (**).
Эти две поверхности показаны на рис. 8.2.
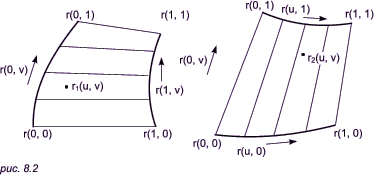
Их сумма r1 + r2 представляет порцию поверхности,
каждая из границ которой является суммой заданной граничной кривой и
прямолинейного отрезка, соединяющего концевые точки этой кривой. Например,
легко проверить с помощью (*) и (**), что граница, соответствующая v = 0,
определяется не вектор-функцией r(u, 0), а выражениемr(u, 0) + .
Тогда если мы можем найти порцию поверхности r3(u, v), границами
которой служат вышеупомянутые прямолинейные отрезки, то можно восстановить
первоначальные граничные кривые, составив выражение
r1 + r2 – r3. Построить r3 легко;
ее границы, отвечающие v = 0 и u = 0, будут даваться выражениями(1 – u)r(0, 0) + ur(1, 0)(1 – u)r(0, 1) + ur(1, 1)соответственно, и последующая линейная интерполяция в v-направлении дастr3(u, v) = (1 – u)(1 – v)r(0, 0) + u(1 – v)r(1, 0) + (1 – u)vr(0, 1) + uvr(1, 1) (***).
Вектор r = r1 + r2 – r3, полученный из
(*), (**) и (***) и определяющий искомую поверхность, удобно представить в
матричном виде:
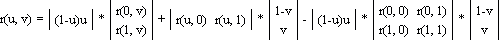
Последовательные подстановки u = 0, u = 1, v = 0 и v = 1 без труда
подтверждают, что порция поверхности, определенная вектором r(u, v), имеет
четыре первоначальные кривые своими границами.
Эта конструкция, использующая только информацию о границах поверхности и
некоторые вспомогательные скалярные функции переменных u и v, определяет
наиболее простой класс поверхностей, первоначально изученный Кунсом (1967),
которые с тех пор известны как поверхности Кунса. Данная здесь трактовка
принадлежит Форресту (1972). Вспомогательные функции u, (1 – u), v и (1 – v)
называются функциями смешения, так как они соединяют воедино четыре отдельные
граничные кривые, чтобы дать одну корректно определенную поверхность.
Огибающая поверхность
Рассмотрим теперь семейство $ \left\{ \mathbf P(\lambda_{}) \right\} $ поверхностей в $ \mathbb R^{3} $, зависящих от параметра $ \lambda_{} $, принимающего значения из интервала $ \in \mathbb R $.
Если существует некоторая поверхность $ \mathbf Q_{} $, которая в каждой своей точке касается некоторой поверхности рассматриваемого семейства, то эта поверхность $ \mathbf Q_{} $ называется огибающей семейства поверхностей $ \left\{ \mathbf P(\lambda_{}) \right\} $.
Видим, что это определение аналогично определению , за одним только исключением: в определении огибающей кривой ставится ограничение на то, что эта кривая не должна совпадать ни с одной кривой семейства на каком-то своем участке, «отрезке». А в определение огибающей поверхности аналогичного требования не приводится. На самом деле, это дополнительное ограничение должно присутствовать — хотя бы для того, чтобы отсечь случай, когда за огибающую поверхность семейства может быть взята любая поверхность этого семейства. Не буду слишком уделять внимания формальностям, считая интуитивно понятным характер ограничения, «дополняющего» определение.
Пусть поверхности семейства $ \left\{ \mathbf P(\lambda_{}) \right\} $ заданы уравнением
$$ \Psi(x,y,z,\lambda)=0 \ , $$
где $ \Psi(x,y,z,\lambda) $ — функция, непрерывно дифференцируемая по своим аргументам. Геометрическое место точек пространства $ (x,y_{},z) $, удовлетворяющих условиям
$$
\Psi(x,y,z,\lambda)=0,\ \frac{\partial \Psi(x,y,z,\lambda)}{\partial \lambda} = 0
$$
называется дискриминантной поверхностью семейства $ \left\{ \mathbf P(\lambda_{}) \right\} $.
П
Пример. Составить уравнение огибающей поверхности системы шаров одинаковых радиусов $ r_{} $,
центры которых лежат на кривой
$$ x=\phi(\lambda), y=\chi(\lambda),z=\psi(\lambda) \, . $$
В частности, получить
уравнение искомой поверхности, если центры шаров лежат на окружности $ x=R \cos \lambda, y=R \sin \lambda, z = 0 $.
Решение. Уравнение семейства шаров:
$$ (x-\phi(\lambda))^2 +(y-\chi(\lambda))^2+(z-\psi(\lambda))^2-r^2=0 \ . $$
Дифференцируем это равенство по параметру $ \lambda_{} $:
$$ (x-\phi(\lambda)) \phi^{\prime}(\lambda) +(y-\chi(t))\chi^{\prime}(\lambda)+(z-\psi(\lambda))\psi^{\prime}(\lambda)=0 \ . $$
Уравнение огибающей поверхности получается исключением параметра $ \lambda_{} $ из этой системы уравнений.
В приведенном частном случае уравнения дискриминантной поверхности:
$$
(x-R \cos \lambda)^2 + (y-R \sin \lambda)^2+z^2-r^2=0,\quad x\sin \lambda – y \cos \lambda =0 \ .
$$
Исключаем $ \lambda_{} $. Из первого уравнения имеем:
$$
(x^2+y^2+z^2+R^2-r^2)=2R(x \cos \lambda+ y \sin \lambda) \ .
$$
Возводим в квадрат:
$$
(x^2+y^2+z^2+R^2-r^2)^2=4R^2(x^2 \cos^2 \lambda+ y^2 \sin^2 \lambda+2 xy \cos \lambda \sin \lambda) \ .
$$
Представим правую часть в виде
$$
4R^2(x^2 (1-\sin^2 \lambda)+ y^2 (1-\cos^2 \lambda)+2 xy \cos \lambda \sin \lambda)=
4R^2(x^2+y^2)-4R^2 (x^2\sin^2 \lambda+ y\cos^2 \lambda-2 x y\cos \lambda \sin \lambda )=
$$
$$
=4R^2(x^2+y^2)-4R^2 (x\sin \lambda – y \cos \lambda)^2 \ .
$$
Теперь воспользуемся вторым из уравнений, задающих дискриминантную поверхность. Уравнение огибающей поверхности:
$$
(x^2+y^2+z^2+R^2-r^2)^2=4\,R^2(x^2+y^2) \ .
$$
Что это за поверхность?
Источники
. Бертранъ Ж. СПб. Изд-во «Наука и жизнь», 1911
. Дингельдэй Фр. СПб. 1912. Типография Суворина
. Рашевский П.К. Курс дифференциальной геометрии. М.Едиториал УРСС, 2003
. Серре И.А. Т.I. М.-СПб. Изданiе т-ва М.О.Вольфъ. 1883
$ \kappa \alpha \upsilon \sigma \tau \iota \kappa \eta $ (древн.греч.) — жгучая, жалящая
Сообщение о замечательных эффектах одного нового зажигательного зеркала.
Может быть также получена как след, заметаемый фиксированной точкой окружности, катящейся без проскальзывания по другой окружности.
evolutus (лат.) — развернутый;
evolvens, (род. падеж evolventis) — разворачивающий
Использование для дифференциальных уравнений
Обыкновенные дифференциальные уравнения
График некоторых решений (y ‘) ^ 2 + xy’-y = 0. Синим цветом обозначены обычные решения, зеленым – особые решения, красным – гибридные решения, упомянутые в тексте.
Дифференциальное уравнение в неявной форме не априори проверить существование и теорему единственности Коши-Липшица. Есть области, в которых мы можем выразить это в форме одного или нескольких явных уравнений, тогда желательно установить связи.
Итак, для уравнения
- (y′)2+Иксy′-yзнак равно{\ displaystyle (y ‘) ^ {2} + xy’-y = 0}
Следует различать три области: параболу и две области, которые она ограничивает. В верхней части уравнение можно представить в одной из двух решаемых форм
yзнак равно-14Икс2{\ displaystyle y = – {\ frac {1} {4}} x ^ {2}}
- y′знак равноy-Иксy′y′знак равно-y-Иксy′{\ displaystyle y ‘= {\ sqrt {y-xy’}} \ qquad y ‘= – {\ sqrt {y-xy’}}}
что дает регулярные решения, выделенные синим цветом на рисунке напротив.
Огибающая этих решений – парабола, нарисованная зеленым цветом, которая составляет решение, квалифицируемое как особое решение. Также существуют «гибридные» решения, образованные путем соединения дуги параболы (зеленый) с правильными решениями (синий). Пример такого решения нарисован красным.
ПРОТИВ1{\ Displaystyle {\ mathcal {C}} ^ {1}}
Что касается теории конвертов, ситуацию лучше всего описать, поместив себя в пространство с дополнительным измерением: пространство ( x , y , y ‘ ).
Уравнения с частными производными первого порядка
При решении дифференциального уравнения в частных производных первого порядка
- F(Икс,y,z,∂z∂Икс,∂z∂y)знак равно{\ displaystyle F \ left (x, y, z, {\ frac {\ partial z} {\ partial x}}, {\ frac {\ partial z} {\ partial y}} \ right) = 0},
мы ищем двухпараметрические семейства поверхностей решений. Такие семейства называются полными интегралами уравнения.
Как и в случае с дифференциальными уравнениями, огибающие (с одним или двумя параметрами) семейств решений также являются решениями. Однопараметрические огибающие называются общими интегралами уравнения; двухпараметрические огибающие являются сингулярными интегралами .
Понятие полного или общего интеграла – понятие относительное. Есть несколько полных интегралов, когда один выбирает один, остальные получаются как общие интегралы.
Дифференциальные преобразования плоских кривых. | |
|---|---|
| Унарная операция | Развёрнутая · эвольвента · двойная кривая · обратная кривая · параллельная кривая (en) · Isoptique |
| Унарная операция, определяемая точкой | Кривая педали · Отрицательная кривая педали · Собачья кривая · Каустик |
| Унарная операция, определяемая двумя точками | Строфоид |
| Бинарная операция, определяемая точкой | Рулетка |
| Операции над семейством кривых | Конверт |



![Огибающая [vmath]](https://debutclub.ru/wp-content/uploads/f/b/f/fbf1e196db1d74cb2f76874015cc1f9f.jpeg)


























![Огибающая [vmath]](https://debutclub.ru/wp-content/uploads/b/1/4/b148f217646e81a51e2ff0955e679d8f.jpeg)