Коэффициент Бергера в шахматах: как его считать?

Примеры форточки в партиях

Еще раз подчеркнем, форточка действует только на открытие. Единожды открыв, мы можем получить такой «сквозняк», что мало не покажется.

Пример:

В данном случае форточка черным не во благо, а во вред.

1.e6!!

У черных катастрофически ослаблены черные поля, что дает белым неотразимую атаку.

Например: 1…fe 2.Фf4 Ce8 3.Фf6! С неотразимыми угрозами.

Итак, подытожим:

Форточка – ход профилактический, чтобы застраховаться от линейного мата по первой (восьмой) горизонтали.

То есть, уместен он тогда, когда угроза мата существует. А именно, при наличии тяжелых фигур у соперника. Согласитесь, совершенно бессмысленно делать форточку, если у соперника остались только легкие фигуры, не способные поставить линейный мат.

Надо ли делать форточку «на всякий пожарный» уже в начале игры?

Из подобных «общих соображений», — точно не надо.

Однако, бывает, что ходы пешками g и h делаются с другими целями – например фиакетирование слона, профилактика связки с поля g5/g4. Или нападение на фигуру с темпом.

В таких случаях ход крайней пешкой имеет тактическую цель. А заодно заблаговременно открывается форточка для короля.

Например:

Ходом пешки черные хотят оттеснить слона белых, заодно делая форточку, которая не будет лишней после рокировки.

Рейтинговые системы, использующие компьютеры в качестве ориентира

Многие рейтинговые системы дают рейтинг игрокам в определенный момент времени, но не могут сравнивать игроков из разных эпох. В 2006 году Матей Гуид и Иван Братко впервые применили новый способ оценки игроков, сравнивая их ходы с рекомендованными ходами шахматного движка . Авторы использовали программу Crafty и утверждали, что даже программа с более низким рейтингом (Elo около 2700) может определить хороших игроков. В своем последующем исследовании они использовали Рыбку 3 для оценки рейтингов шахматистов.

В 2017 году Жан-Марк Аллиот сравнил игроков, использующих Stockfish 6, с рейтингом ELO около 3300, что намного выше, чем у лучших игроков-людей.

Женщины, парный разряд

Самый длинный обычный тай-брейк

Николь Пратт и Брайан Стюарт победили Корину Морариу и Ренне Стаббс 7–6 (7–5) , 7–6 (22–20) в первом раунде турнира на острове Амелия в 2006 году.

Другие длинные тай-брейки

Маниша Малхотра и Сания Мирза выиграли тай-брейк 21–19 у Влады Экшибаровой и Иванны Исраиловой в парном матче Кубка Федерации 2004 года Азия-Океания . Малхотра и Мирза выиграли 7–6 (21–19) , 6–1.
Розмари Казалс и Кэтлин Хорват победили Сэнди Коллинз и Бет Херр 5–7, 6–1, 7–6 (20–18) во втором раунде чемпионата Липтона 1984 года WTA .
Манон Боллеграф и Зина Гаррисон выиграли тай-брейк 18–16 у Кристины Сингер и Ирины Спирли в Кубке Фольксвагена 1994 года . Певица и Спирлея выиграли матч 7–6 (7–2) , 6–7 (16–18) , 6–4.
Ламис Алхусейн Абдель Азиз и Анастасия Золотарева победили Пиа Ловрич и Саумья Виг со счетом 7–6 (18–16) , 6–3 в первом раунде турнира ITF W15 в Каире 8 декабря 2020 года. Они выиграли первый сет в четвертом сете. поставил точку, сохранив против них семерых.

Самый длинный тай-брейк матча

Мерел Хоэдт и Александра Райли победили Лорен Купер и Дакоту Фордхэм со счетом 4–6, 6–3, в первом раунде ITF $ 15 000 SA Spring Open в Йоханнесбурге 24 сентября 2019 года. Один тай-брейк длился 34 минуты. с каждой парой по восемь матчевых очков. Первая тройка Купера и Фордхэма пришлась на 9–6.

Другие тай-брейки на длительные матчи

Бетани Маттек и Владимира Улиржова победили Джилл Крайбас и Микаэллу Крайчек 5–7, 6–4, в первом раунде чемпионата Бауш и Ломб 2008 года .
Гизела Дулко и Флавия Пеннетта победили Эдину Галловиц и Барбору Захлавову-Стрицову 4–6, 6–2, в полуфинале Кубка мира 2009 Sony Ericsson Colsanitas .
Ингрид Нил и Мария Санчес победили Алексу Гуарачи и Эрин Рутлифф 6–2, 1–6, в четвертьфинале турнира Boyd Tinsley Clay Court Classic 2018 года . Рутлифф также победил Алекса Глатч 7–5, 3–6, в одиночном разряде в Риме , Джорджия, США, 25 января 2021 года.
Жанетт Хусарова и Мария Кириленко победили Джилл Крайбас и Аллу Кудрявцеву 6–2, 5–7, в первом раунде Aegon International 2009 .
Жаклин Кабаж Авад и Мелани Клаффнер победили Совджанью Бависетти и Ван Данни со счетом 2–6, 6–4, в первом раунде ITF на чемпионате ITF Gwalior среди женщин за $ 25 000 12 ноября 2019 г. Они выиграли седьмое матч-пойнт. в тай-брейке (первое наступление со счетом 10–9), спасая троих от Бависетти и Ванга, первый из которых был при счете 8–9.
Aiko Nakamura и Camille Pin победили Лигу Декмейере и Ипки Шенола 1-6, 6-2, в первом раунде 2007 Банка Вест Классик .
Алиса Клейбанова и Екатерина Макарова победили Камиллу Пин и Орели Веди со счетом 2–6, 6–4, в четвертьфинале Гран-при 2009 года в ЮАР La Princesse Lalla Meryem .
Сара Эррани и Роберта Винчи обыграли Анну-Лену Грёнефельд и Квету Пешке 7–5, 2–6, в четвертьфинале Международного Сиднейского чемпионата Апиа 2013 .
Джорджия Крэчун и Жаклин Кристиан обыграли Екатерину Казионову и Екатерину Шалимову 6–4, 4–6, в четвертьфинале ITF Мемориального кубка Марата Зверева с бай-ином $ 25 000 в Минске , Беларусь, 13 июня 2019 года. третий матч-пойнт на тай-брейке (первое при счете 10–9), спасший шесть от Казионовой и Шалимовой, первое из которых было при счете 8–9.
Хироко Кувата и Киока Окамура победили Эбби Майерс и Белинду Вулкок со счетом 5–7, 6–2, в четвертьфинале ITF Brisbane QTC Tennis International с бай-ином $ 25 000 2 октября 2019 года. тай-брейк (первый приход на 10–9), спас трех от Майерса и Вулкока, первый из которых был на 8–9.
Барбора Миклова и Каролина Беранкова обыграли Алену Фомина и Дарью Кружкову со счетом 3–6, 6–3, в четвертьфинале ITF Milovice Indoor Open с бай- ином $ 15 000 28 ноября 2019 года. Они выиграли по пятому матчевому очку. -брейкер (первый выход на 10–9), спас четверых от Фомина и Кружковой, первый из которых – 8–9.
Кэтрин Харрисон и София Уиттл победили Аллуру и Марибеллу Замаррипу со счетом 5–7, 6–3, в первом раунде турнира по теннису в Риме , Джорджия, США, с бай-ином $ 60 000 , в Риме , штат Джорджия, США, 26 января 2021 года. их шестой матч-пойнт на тай-брейке (первый – 10–9), спас трех от близнецов Замаррипы, первый из которых был при 8–9.
Елена Милованович и Ноэлия Зебаллос Мельгар победили Юку Хосоки и Нану Кавагиси 3–6, 6–3, в полуфинале турнира ITF с бай-ином $ 15 000 в Монастире , Тунис, 10 сентября 2021 года. Они выиграли в своем четвертом матче. очко на тай-брейке (первое наступление – 10–9), спасая пять от Хосоки и Кавагиси, первый из которых был при 8–9.

Олимпийские игры

Сюй Ифань и Ян Чжаосюань победили Александру Крунич и Нину Стоянович 4–6, 6–4, в первом раунде Олимпийских игр 2020 года в Токио . Они выиграли свой седьмой матч-пойнт, сэкономив два при 8–9 и 10–11.

Распространенные ошибки

От них не застрахован никто, но надо о них знать, чтобы не попасть в подобную ситуацию. Ведь мудрые учатся на чужих ошибках.

Попадание в цейтнот

Самое трудное в тай-брейке – это реализовать перевес. Укороченное время не дает времени на тщательное обдумывание ходов. Совершенно некогда реализовывать сильную и красивую партию. Надо выигрывать уже выигранную позицию, как говорят шахматисты. То есть нельзя расслабляться, выиграв ход, надо приложить все силы для удержания победы.

Следует помнить, что при попадании в цейтнот, шахматист может начать игру таким образом, чтобы вынудить и соперника уйти туда же. Не следует попадаться на эту уловку, надо вести игру в соответствии со своими планами, а не планами противника.

Счет длинных вариантов

Нельзя переоценивать свои силы и недооценивать соперника. В любой момент тай-брейка все может измениться. Поэтому рассчитывать длинные варианты – заведомо ошибочная стратегия, которая приведет к краху всей партии.

Главное в тай-брейке для победы – не допускать грубых ошибок и добиться, чтобы просчёты совершал противник.

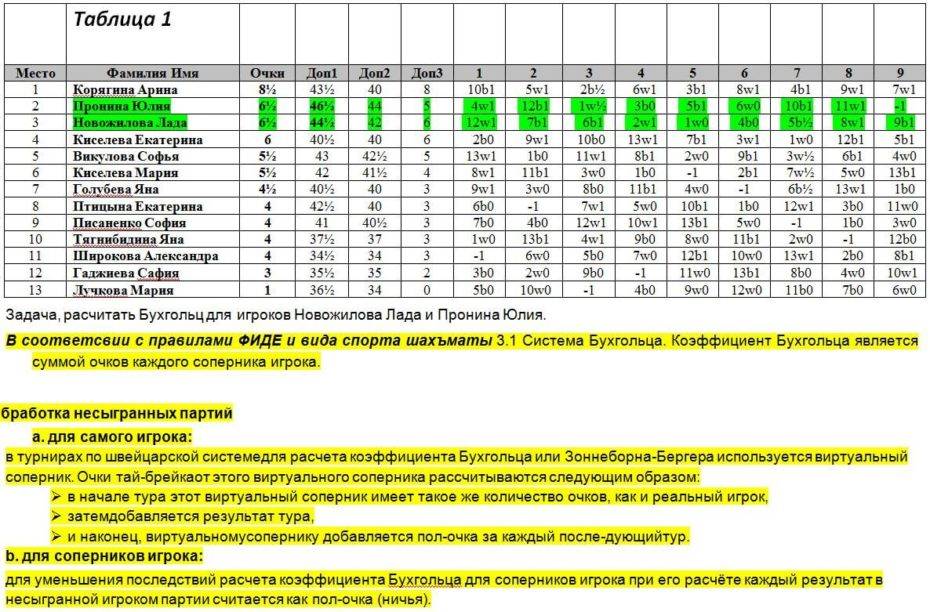
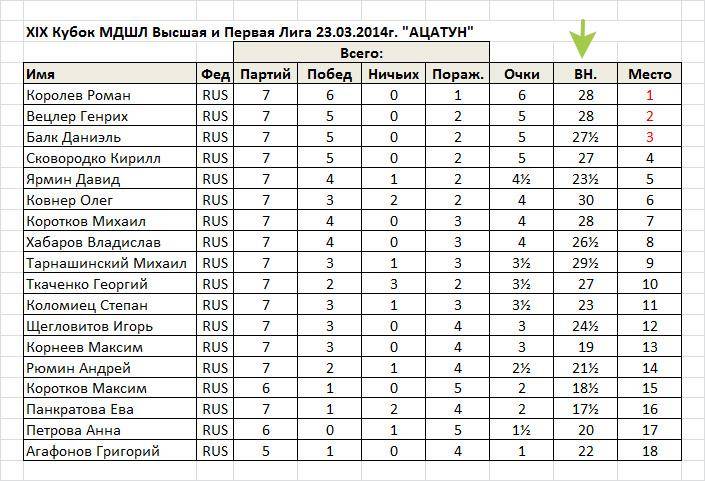
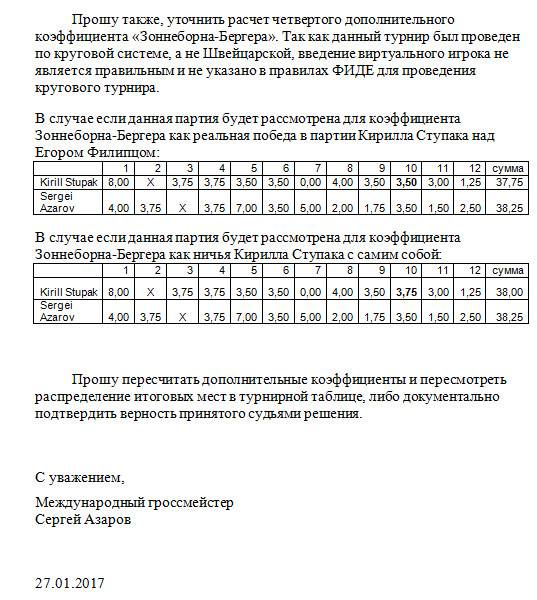
Усеченный коэффициент Бухгольца

Если у двух или более участников оказываются равными и количество набранных очков, и коэффициенты Бухгольца, то из коэффициента Бухгольца каждого участника вычитают результат соперника с меньшим количеством очков. Если после такого вычитания коэффициенты Бухгольца (без результата соперника с меньшим количеством очков) остаются равными, то процедура повторяется, то есть вычитают результат следующего слабейшего соперника и т.д.

Коэффициенты Бухгольца и Бергера изначально применялись только в турнирах по шахматам, однако, затем широко распространились и на другие игры, в которых результат строго фиксирован по набранным очкам (победа, поражение или ничья).

Примечание. К вопросу о расчете коэффициентов при пропуске тура и неявке соперника.

Как правило, используется следующий подход.

Все несыгранные партии (пропуск тура, неявка или нехватка соперника, “плюс”) в целях подсчета коэффициентов условно считаются ничейными:

при неявке соперника партия условно счичается ничейной
при отсуствии соперника (при нечетном числе участников в швейцарской системе) партия считается сыгранной вничью с самим собой
при пропуске тура в начале турнира (при опоздании) или в конце турнира (при снятии) считается, что партии сыграны вничью с самим собой

Данные меры часто необходимы, чтобы сравнивать коэффициенты участников, сыгравших разное количество партий. В противном случае, возможен вариант, например, когда один из участников набирает 7 из 10 и занимает 1 место, а второй – 7 из 7, обыграв лидера, остается только на 2 месте… начав с 4 тура, он будет иметь заведомо более низкий коэффициент. При начислении бухгольца за пропущенные туры, игрок со 100% результатом, вероятно, выйдет на 1 место, что является более справедливым.

Кумулятивная

Чтобы рассчитать это, просуммируйте текущий счет для каждого раунда. Например, если у игрока (по порядку) есть выигрыш, проигрыш, выигрыш, ничья и проигрыш; его счет за раунд будет 1, 1, 2, 2½, 2½. Сумма этих чисел составляет 9. Кроме того, одно очко вычитается из суммы за каждый неигранный выигрыш и ½ очка вычитается за каждый неигранный розыгрыш. В предыдущем примере, если бы ничья в четвертом раунде была вместо ½ балла до свидания, то вычиталось бы ½ балла, и окончательная сумма составляла бы 8½.

Эта система придает больший вес играм, выигранным в первых раундах, и меньше всего – играм, выигранным в финальных раундах. Обоснование этой системы заключается в том, что игрок, который хорошо забил в начале турнира, скорее всего, столкнулся с более сильными соперниками в последующих раундах и, следовательно, должен иметь преимущество перед игроком, который плохо забил в начале, прежде чем впоследствии набрать очки против более слабых соперников ( : 200–201).

Конечно, в век компьютеров и смартфонов, вместо того, чтобы накапливать очки, набранные против слабых игроков, мы могли просто подсчитать, у кого был самый жесткий график, как в случае с системой Солкова и медианной системой. Альтернативное объяснение популярности накопительной системы состоит в том, что тренерам, игрокам и аудитории легче следить за потенциальными счетами и призами, поскольку общее количество очков не меняется, и их нужно только добавлять от раунда к раунду.

Порядок вычисления

В круговых турнирах, где за победу, ничью и поражение присуждается определённое постоянное число очков (например, в шахматах за победу даётся 1 очко, за ничью – 0,5 очка, за поражение – 0 очков), часто случается так, что два или несколько участников набирают одинаковое количество очков. Чтобы определить, кто из этих участников занял более высокое место, подсчитывают коэффициенты Бергера участников.

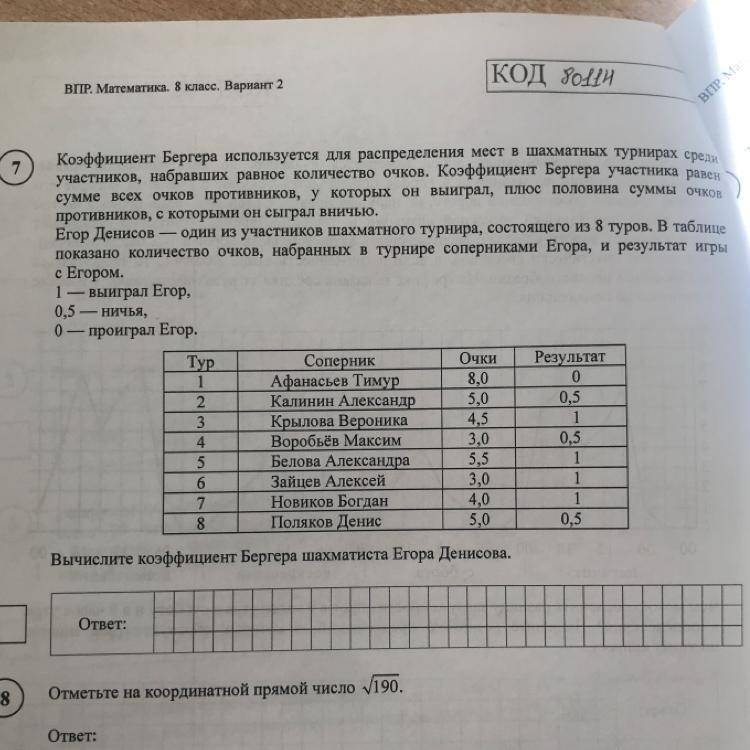
Коэффициент Бергера определённого участника складывается из суммы всех очков противников, у которых данный участник выиграл, плюс половина суммы очков противников, с которыми данный участник сыграл вничью. Идея, на которой базируется коэффициент: из двух участников, равных по числу очков, сильнее тот, кто выиграл у более сильных противников, то есть у тех, кто набрал больше очков. Поэтому участнику, имеющему больший коэффициент Бергера, присуждается более высокое итоговое место в турнире.

Коэффициент Бергера придуман для круговых турниров, но может, при необходимости, применяться и в других схемах розыгрыша, где игроками, места которых надо распределять, играется равное число партий. Можно его использовать и в турнирах по швейцарской системе , хотя традиционно там применяется коэффициент Бухгольца . В круговых турнирах с 1985 года применяется и «упрощённый Бергер» (предложен М.Дворецким): очки всех соперников, у кого шахматист выиграл, берутся со знаком «плюс», а всех, кому он проиграл – со знаком «минус», по сумме и считается лучший результат. Это позволяет сократить расчёты и не делить предварительно пополам большинство результатов.

Стратегия и тактика тай-брейка

Есть несколько рекомендаций по проведению партии с укороченным временем.

Лучшее — враг хорошего

Все поиски, среди которых и определение сильнейшего хода, и лучшего плана, и прекрасной комбинации лучше оставить для обычной, классической игры. Это лишь будет потерей времени, которого и так немного.

Удивите своего соперника

Мастера шахмат всегда имеют план на любой случай. Поэтому у них в запасе всегда есть дебютная заготовка, которая заставит нервничать соперника. Противнику придется играть точно и быстро, а это может привести к неминуемым ошибкам, которыми можно воспользоваться.

Пример

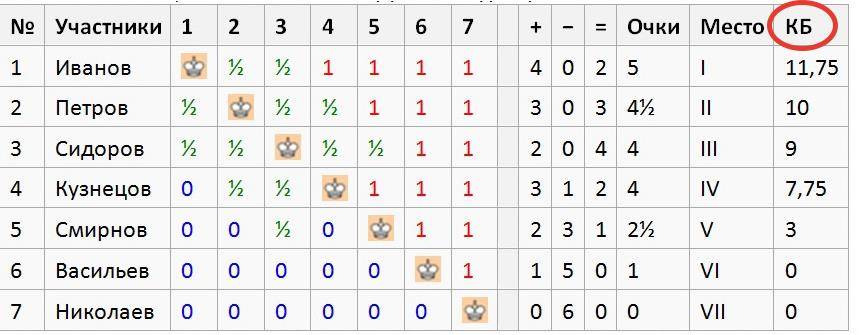
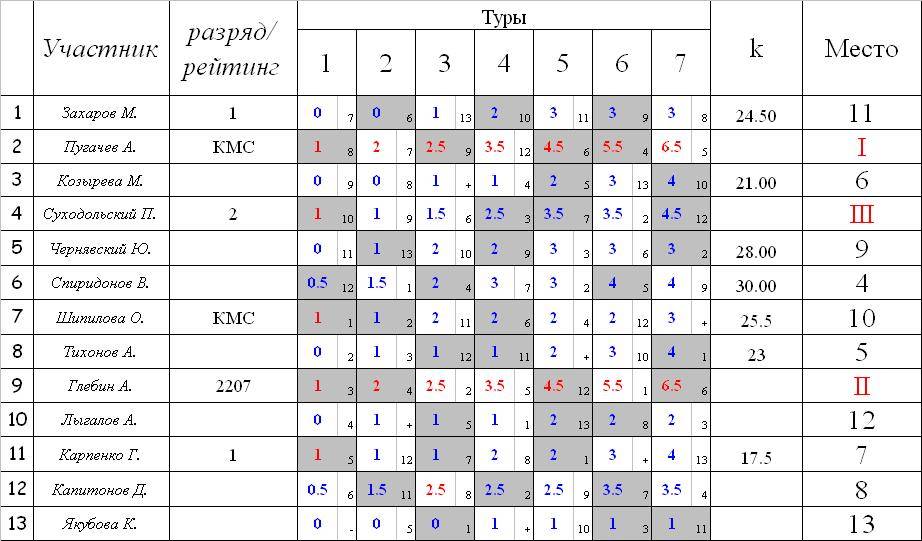
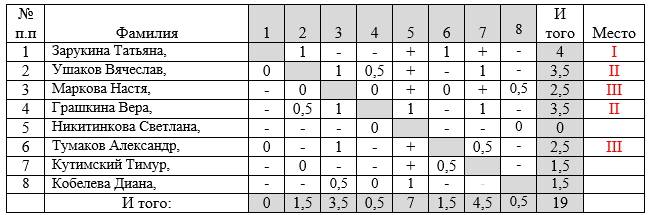
Итоговая таблица гипотетического кругового турнира:

№	Участники	1	2	3	4	5	6	7		+	−	=	Очки	Место
1	Иванов		½	½	1	1	1	1		4	2	5	I	11,75
2	Петров	½		½	½	1	1	1		3	3	4½	II	10
3	Сидоров	½	½		½	½	1	1		2	4	4	III	9
4	Кузнецов	½	½		1	1	1		3	1	2	4	IV	7,75
5	Смирнов	½		1	1		2	3	1	2½	V	3
6	Васильев		1		1	5	1	VI
7	Николаев			6	VII

Обозначения: 1 – победа, ½ – ничья, 0 – поражение, КБ – коэффициент Бергера.

Участники Сидоров и Кузнецов набрали одинаковое количество очков, по 4 очка. Кто из них займет третье место, решается по коэффициенту Бергера.

Коэффициент Бергера участника Сидорова складывается так: 2,5 (половина очков Иванова) + 2,25 (половина очков Петрова) + 2 (половина очков Кузнецова) + 1,25 (половина очков Смирнова) + 1 (все очки Васильева) + 0 (все очки Николаева) = 9.

Коэффициент Бергера участника Кузнецова так: 0 (за поражение от Иванова) + 2,25 (половина очков Петрова) + 2 (половина очков Сидорова) + 2,5 (все очки Смирнова) + 1 (все очки Васильева) + 0 (все очки Николаева) = 7,75.

Таким образов участник Сидоров имеет более высокий коэффициент Бергера чем участник Кузнецов (9 против 7,75), поэтому третье место присуждается Сидорову.
Коэффициент Бергера более высок у того, кто выигрывает или добивается ничьей с более сильными игроками (игроками набирающими большее количество очков). В приведённом примере выигрыш у участника, имеющего ноль очков, не даёт вклада в коэффициент Бергера.

Система Харкнесса

Эта система была отмечена в Chess Review организатором турниров Кеннетом Харкнессом , который 14 лет спустя изложил свое изобретение этой системы в статьях 1956 года. Он использовался USCF с 1950 по 1960 год и другими лигами.

Когда игроки участвуют в турнире, рассчитывается средний рейтинг их соревнований. Если игрок набирает 50%, он получает средний рейтинг соревнований в качестве рейтинга его выступлений. Если они набирают более 50%, их новый рейтинг равен среднему значению соревнования плюс 10 очков за процентный пункт, превышающий 50. Если они набирают меньше, их новый рейтинг равен среднему значению соревнования минус 10 очков за процентный пункт меньше 50 ( : 185 –88)

Пример

Игрок с рейтингом 1600 играет в турнире из одиннадцати туров и набирает 2½ – 8½ (22,7%) против соперников со средним рейтингом 1850. Это на 27,3% ниже 50%, поэтому его новый рейтинг 1850 – (10 × 27,3) = 1577 ( : 187).

Порядок вычисления[]

В круговых турнирах, где за победу, ничью и поражение присуждается определённое постоянное число очков (например, в шахматах за победу даётся 1 очко, за ничью — 0,5 очка, за поражение — 0 очков; реже — 3 — за победу и 1 за ничью, например, в London Chess Classic 2010), часто случается так, что два или несколько участников набирают одинаковое количество очков. Чтобы определить, кто из этих участников занял более высокое место, подсчитывают коэффициенты Бергера участников.

Коэффициент Бергера придуман для круговых турниров, но может, при необходимости, применяться и в других схемах розыгрыша, где игроками, места которых надо распределять, играется равное число партий. Можно его использовать и в турнирах по швейцарской системе, хотя традиционно там применяется коэффициент Бухгольца. В круговых турнирах с 1985 года применяется и «упрощённый Бергер» (предложен М.Дворецким): очки всех соперников, у кого шахматист выиграл, берутся со знаком «плюс», а всех, кому он проиграл — со знаком «минус», по сумме и считается лучший результат. Это позволяет сократить расчёты и не делить предварительно пополам большинство результатов.

Приложение 2. Таблицы Варма

1. Арбитр должен заранее подготовить конверты без опознавательных знаков, каждый из которых содержит один из наборов чисел А, В, С и D, как указано ниже в пункте 5. Эти конверты затем соответственно помещаются в конверты большего размера, на каждом из которых указывается количество номеров игроков, содержащихся в малых конвертах.

2. Заранее составляется следующий список порядка, в котором игроки тянут жребий: в первую очередь тянут жребий игроки из федерации с наибольшим числом предста-вителей. Если две или более федерации имеют одинаковое количество представи-телей, очередность определяется в алфавитном порядке кода страны в ФИДЕ. Сре-ди игроков одной федерации очередность определяется в алфавитном порядке их фамилий.

3. Например, первый игрок федерации с наибольшим числом игроков должен выбрать один из больших конвертов, содержащий по крайней мере достаточно номеров для представителей своей федерации, а затем вытянуть из этого конверта один из номе-ров. Остальные игроки из той же федерации также вытягивают свои номера из того же конверта. Оставшиеся номера будут выбраны другими игроками.

4. Затем выбирают конверт игроки следующей федерации, и процедура повторяется до тех пор, пока все игроки не выберут свои номера.

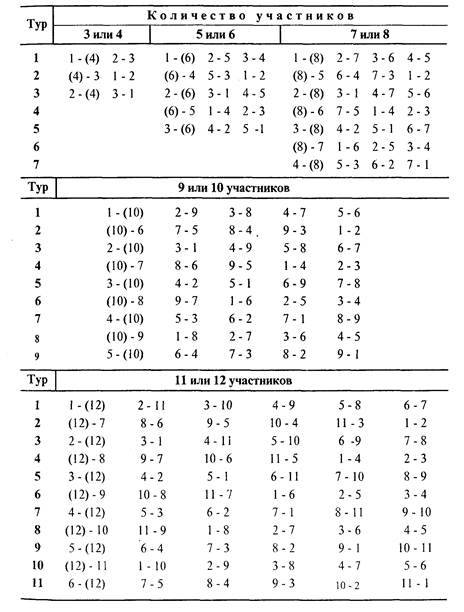
5. Следующие таблицы Варма могут быть использованы для количества игроков от 9 до 24.

9/10 игроков 11/12 игроков 13/14 игроков

A: (3, 4, 8) A: (4, 5, 9, 10) A: (4, 5, 6, 11, 12)

B: (5, 7, 9) B: (1, 2, 7) B: (1, 2, 8, 9)

C: (1, 6) C: (6, 8, 12) C: (7, 10, 13)

D: (2, 10) D: (3, 11) D: (3, 14)15/16 игроков 17/18 игроков 19/20 игроков

A: (5, 6, 7, 12, 13, 14) A: (5, 6, 7, 8, 14, 15, 16) A: (6, 7, 8, 9, 15, 16, 17, 18)

B: (1, 2, 3, 9, 10) B: (1, 2, 3, 10, 11, 12) B: (1, 2, 3, 11, 12, 13, 14)

C: (8, 11, 15) C: (9, 13, 17) C: (5, 10, 19)

D: (4, 16) D: (4, 18) D: (4, 20)21/22 игрока 23/24 игрока

A: (6, 7, 8, 9, 10, 17, 18, 19, 20) A: (6, 7, 8, 9, 10, 11, 19, 20, 21, 22)

B: (1, 2, 3, 4, 12, 13, 14, 15) B: (1, 2, 3, 4, 13, 14, 15, 16, 17)

C: (11, 16, 21) C: (12, 18, 23)

Система Зоннеборна – Бергера
– метод определения лучшего результата (коэффициента) в случае, если несколько участников турнира набрали одинаковое количество очков. Коэффициент участников равен сумме очков противников, у которых они выиграли, и половины очков противников, с которыми они сыграли вничью.

Фактически системой коэффициентов Зоннеборна – Бергера отдает преимуществу игроку, который выигрывал у сильных игроков и проигрывал слабым перед «нормальным» игроком, который проигрывал сильным и выигрывал у слабых. Коэффициенты Зоннеборна – Бергера широко применяются, особенно в круговых турнирах.

Система Зоннеборна – Бергера не является объективной, поэтому в важных случаях (определение чемпиона, допуск в следующий этап крупного соревнования) принято проводить дополнительное соревнование. Применяется и смешанный метод (при равенстве очков в дополнительном соревновании решает коэффициент Зоннеборна – Бергера).

Наряду с системой коэффициентов Зоннеборна – Бергера применяются другие методы выявления преимущества при равенстве очков: по числу побед, по результату встречи между собой и др.

Расчет значения российского рейтинга для спортсмена на день окончания спортивного соревнования

Расчет значения российского рейтинга для спортсмена на день окончания спортивного соревнования осуществляется по следующей формуле: Rо=Rн+ ΣΔR х K, где:

Rо – значение российского рейтинга на день окончания спортивного соревнования;

Rн – значение российского рейтинга на день начала спортивного соревнования;

ΣΔR х K – изменение значения российского рейтинга по результатам спортивного соревнования;

ΣΔR – сумма разностей для каждой фактически сыгранной партии;

ΔR – разность для каждой фактически сыгранной партии рассчитывается по формуле: ΔR = N – PD,

где:

N – количество очков, набранных в партии (1 или 0,5 или 0);

PD – вероятность выигрыша, определяемая по Таблице преобразования разности российских рейтингов играющих между собой спортсменов, имеющих более высокий российский рейтинг и более низкий российский рейтинг;

K – коэффициент развития, соответствующий диапазону значений российского рейтинга:

Диапазон значений российского рейтинга	Коэффициент развития (К)
1000-1199	60
1200-1399	50
1400-1599	40
1600-1799	35
1800-1999	30
2000-2199	25
2200-2399	20
>=2400	10

Счет Зоннеборна – Бергера

Сложите очки каждого оппонента, которого бьет игрок, и половину очков каждого оппонента, которого набрал игрок ( : 201). Система была названа в честь Уильяма Зоннеборна и Иоганна Бергера , но была изобретена Оскаром Гельбфусом ( : 137). Эта система является основной системой определения ничьей в круговых турнирах , но также используется в швейцарских турнирах. Ее также называют партитурой Нойштадтля .

То, что мы называем системой Зоннеборна-Бергера, не было изобретено ни Зоннеборном, ни Бергером, и изначально она не предназначалась для разрешения споров. Он был изобретен Оскаром Гельбфусом около 1873 года для использования в качестве взвешенного счета в круговых турнирах. Он будет использоваться вместо исходной оценки за финальные места. В 1886 году Соннеборн раскритиковал систему и предложил улучшение, которое дало бы более взвешенную оценку. Его предложение состояло в том, чтобы добавить квадрат очков игрока к сумме, рассчитанной, как указано выше. В 1887 и 1888 годах Бергер изучал систему Гельбфуха и предложение Зоннеборна. Это усовершенствование стало известно как система Зоннеборна-Бергера.

Когда система используется для разрыва связей между игроками, набравшими одинаковое количество очков, добавление квадрата исходного результата игрока не приносит никакой пользы, поэтому улучшение Зоннеборна опускается. Однако система сохранила название Зоннеборна-Бергера ( : 136–37).

Пример

Итоговая таблица гипотетического кругового турнира:

№	Участники	1	2	3	4	5	6	7		+	−	=	Очки	Место
1	Иванов		½	½	1	1	1	1		4	2	5	I	11,75
2	Петров	½		½	½	1	1	1		3	3	4½	II	10
3	Сидоров	½	½		½	½	1	1		2	4	4	III	9
4	Кузнецов	½	½		1	1	1		3	1	2	4	IV	7,75
5	Смирнов	½		1	1		2	3	1	2½	V	3
6	Васильев		1		1	5	1	VI
7	Николаев			6	VII

Обозначения: 1 – победа, ½ – ничья, 0 – поражение, КБ – коэффициент Бергера.

Таким образов участник Сидоров имеет более высокий коэффициент Бергера чем участник Кузнецов (9 против 7,75), поэтому третье место присуждается Сидорову. Коэффициент Бергера более высок у того, кто выигрывает или добивается ничьей с более сильными игроками (игроками набирающими большее количество очков). В приведённом примере выигрыш у участника, имеющего ноль очков, не даёт вклада в коэффициент Бергера.

Коэффициент Бергера

Коэффициент Бергера – способ определения мест (дополнительный коэффициент) в соревнованиях среди участников, набравших равное количество очков в основном турнирном зачете. Применяется в играх, где за победу, ничью и поражение присуждается определенное постоянное число очков (например, 1, 0.5 и 0 – в шахматах, шашках, Го, рэндзю и т.д.).

Первым такую систему подсчета очков при распределении мест предложил чехословацкий шахматный мастер Оскар Гелбфус (Oskar Gelbfuhs) в августе 1873 года.

Коэффициент Бергера был первоначально разработан для круговых шахматных турниров, где каждый участник играет с каждым. Позже этот метод стали применять и для соревнований по другим играм, например, Го.

На практике коэффициент Бергера впервые применили Уильям Зонненборн (William Sonneborn) и Иоганн Бергер (Johann Berger) на турнире в Ливерпуле в 1882 году. В 1886 году распределение мест по коэффициенту Бергера было введено в регулярную практику.

Коэффициент Бергера определенного участника складывается из суммы всех очков противников, у которых данный участник выиграл, плюс половина суммы очков противников, с которыми данный участник сыграл вничью. Идея, на которой базируется коэффициент: из двух участников, равных по числу очков, сильнее тот, кто выиграл у более сильных противников, то есть у тех, кто набрал больше очков. Поэтому участнику, имеющему больший коэффициент Бергера, присуждается более высокое итоговое место в турнире.

Коэффициент Бергера придуман для круговых турниров, но может, при необходимости, применяться и в других схемах розыгрыша с равным числом партий, например, в турнирах по швейцарской системе (хотя традиционно там применяется коэффициент Бухгольца).

Что такое коэффициент Бергера в шахматах?

Примеры форточки в партиях

Рейтинговые системы, использующие компьютеры в качестве ориентира