Как хранить базу решений
Каким способом хранить найденную базу решений?
Самый простой и неправильный способ — использовать сериализацию. Засериализованный четырёхмерный массив структуры занял 1.7 гигабайта(!) на диске. Процесс сериализации длился минут шесть, на десериализацию потребовалось примерно столько же.
Такой вариант, ясное дело, не подходит. К тому же, на практике нет надобности использовать весь четырёхмерный массив. Для конкретной позиции нужна только одна запись.
Для экономии места ещё можно избавиться от хранения координат фигур для каждой комбинации! Когда у нас есть четырёхмерный массив, то позиция каждой фигуры на доске однозначно определяется её индексом в массиве.
Было решено хранить всю базу решений в одном файле — как линейную развёртку четырёхмерного массива. Для любой возможной позиции вычисляется адрес, по которому записан правильный ответ.
Как максимально компактно записать нужный нам ответ? Позицию фигур хранить не надо, поэтому остаётся только три числа — сколько ходов до мата, чем ходить и куда ходить. Именно так однозначно определяется правильный ход за белых.
5 бит. Сколько ходов до мата — это целое число от 0 до 33.
2 бита. Какая фигура ходит — три возможных варианта, король, слон или конь.
6 бит. Куда фигура ходит — индекс поля на доске от 0 до 63.
Значит, на каждую запись решения достаточно два байта:
1 байт — сколько ходов до мата, или 0, если позиция незнакомая.
2 байт — FFNNNNNN
FF — номер фигуры, которой нужно ходить (1 — король, 2 — слон, 3 — конь)
NNNNNN — координата клетки — куда ходить (от 0 до 63).
Итак, файл базы решений занимает 64 * 32 * 64 * 64 слов = ровно 16 мегабайт. Размещение фигур задаётся координатами каждого слова, в первом байте — количество ходов до мата (или 0 если решения нет), во втором байте хранится правильный ход.
Можно было бы ещё в два раза уменьшить размер файла, если не хранить количество ходов до мата, но так играть будет не интересно.
Сколько всего вариантов?
На шахматной доске 64 клетки. У нас четыре фигуры. Количество возможных комбинаций — 64 * 64 * 64 * 64 = 16,777,216.
Можно оставить только белопольного слона. Количество вариантов уменьшится вдвое: 64 * 32 * 64 * 64 = 8,388,608. Именно столько позиций будет в нашей базе решений.
На самом деле комбинаций ещё меньше: на одной клетке не может стоять две фигуры, короли не могут стоять на соседних клетках, чёрный король не может быть под шахом и так далее. Забегая вперёд скажу, что в базе решений оказалось 5,609,790 комбинаций, массив будет заполнен на 67%.
Однако для упрощения алгоритма и ускорения доступа к данным базы я решил «не мелочиться» и создать четырёхмерный массив для всех комбинаций.
Для хранения каждой комбинации определена такая структура:
Внутри используется ещё одна структура Coord для записи координат фигуры, с возможностью вычисления индекса от 0 до 63, а также с перегруженным оператором сравнения.
Эта структура оказалась очень удобной для передачи в качестве аргумента в различные вспомогательные функции, например:
Однако для записи результата базы решений этой структуры не достаточно, ещё нам потребуется…
Координаты чёрнопольного белого слона
Пришло время платить за оптимизацию. Нужно реализовать алгоритм пересчёта координат для комбинаций с «чёрно-белым» слоном.
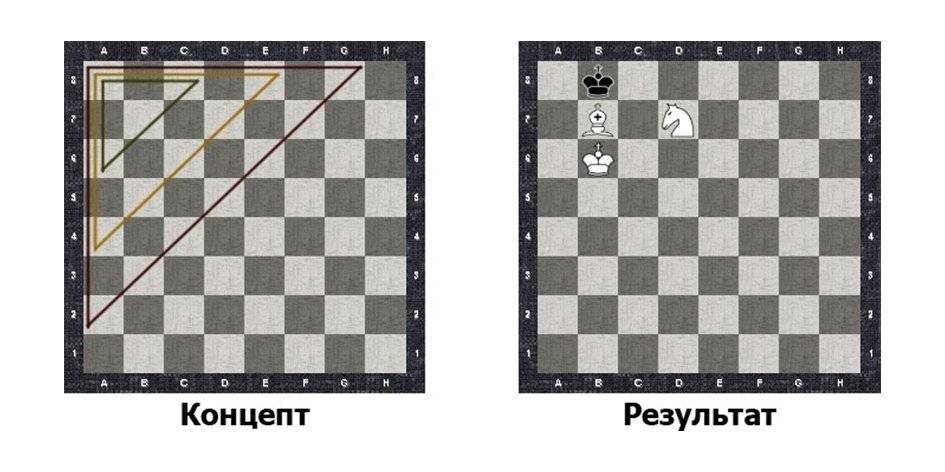
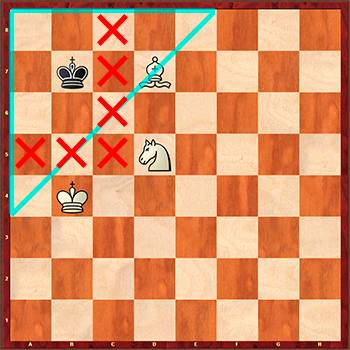
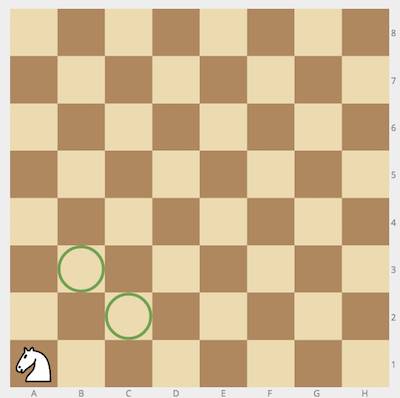
Это было сделано следующим образом. Если координата слона попадает на чёрное поле, то необходимо координаты всех фигур на доске «перевернуть». При этом координата Y остаётся неизменной, а X меняется на 7-X. Наглядная демонстрация переворота координат см. на рисунке.
Если слон стоит на белой клетке, то санчала необходимо «перевернуть» координаты всех фигур. Потом искать позицию в базе решений. И ещё раз «перевернуть» считанную оттуда координату правильного хода.